티스토리 뷰
t-검정 절차
1) 귀무가설과 대립가설을 설정
2) 유의수준(α) 결정 – 양측검정과 단측검정을 결정
3) 검정통계량 계산
4) 조사결과에 대한 유의확률(p값) 계산
5) 결정했던 유의수준과 유의확률을 비교하여 통계적 유의성 판단
단일 표본 평균에 대한 t-검정
단일 모집단 평균에 대한 검정 3가지의 가설 설정과 검정 방법
귀무가설은 모집단의 평균이 특정값과 같다입니다.
대립가설은 아래와 같이 3가지의 가설 설정이 가능합니다.
1. 모집단의 모평균(μ)이 특정값(μ0)보다 작다. 좌측검정(left-sided test)
2. 모집단의 평균(μ)이 특정값(μ0)보다 크다 우측검정(right-sided test)
3. 모집단의 평균(μ)이 특정값(μ0)과 같지 않다. 양측검정(two-sided test)
[설명] 단일 모집단 평균에 대한 검정을 위해 3가지의 대립가설을 설정할 수 있습니다.
첫 번째는 모집단의 모평균이 특정값(μ0)보다 작다는 가설,
두 번째는 모집단의 평균이 특정값(μ0)보다 크다는 가설,
세 번째는 모집단의 평균이 특정값(μ0)과 같지 않다는 가설을 세울 수 있습니다.
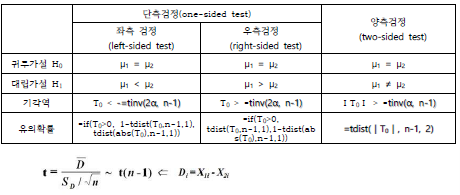
이때 각각을 검정하는 방법을 좌측검정(left-sided test), 우측검정(right-sided test), 양측검정(two-sided test)이라고 하며, 좌측검정과 우측검정을 합하여 단측검정 (one-sided test)이라고 합니다.
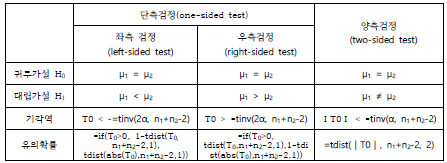
각각의 가설에 대한 기각역(rejection region) 형태를 정리하면 다음과 같습니다.

엑셀에서 단일모집단 평균을 검정하는 방법은 2가지가 있습니다.
첫 번째는 검정통계량과 기각치, 그리고 유의확률을 각각 엑셀 함수를 이용하여 계산하는 방법과 두 번째는 메뉴탭에서 데이터 분석 → ‘t-검정 : 쌍체 비교’를 선택해서 처리하는 방법이 있습니다.
두 번째 방법인 분석도구를 이용한 t-검정은 방법이 매우 간단합니다. 단, 검정결과도간단하게 보이기 때문에 결과를 이해하기 위해 직접 함수를 이용하여 T-검정의 통계량과 유의확률, 기각역을 구해보도록 하겠습니다.
엑셀 함수로 t-검정
엑셀 함수를 이용하여 검정통계량과 기각역, 유의확률을 구하는 검정 절차를 수행하기 위해서는 먼저 검정통계량의 분포를 선택해야 하는데 모집단의 분산(σ2)을 아는 경우에는 검정통계량 Z0 = (표본평균–귀무가설 검증값) / (표준편차/표본수의 제곱근)이 평균과 분산이 각각 0과 1인 표준정규분포를 따르기 때문에 Z0 통계량 값을 사용합니다.

그러나 모집단의 분산을 모를 시는 표본 분산(s2)을 사용하는데 이때는 자유도가 (n-1)인 t-분포를 따르는 T0 통계량을 사용합니다.

그런데 표본 조사 시 일반적으로는 모집단의 분산을 모르는 경우가 대부분이므로 T0 통계량을 주로 사용합니다. 이 검정통계량의 분포 이론은 모집단이 정규분포라는 가정하에서 유도되었기 때문에 데이터에 심각한 특이치가 있는 경우에는 다른 분석방법을 적용하는 것이 적절합니다.
t-분포에 따르는 검정통계량을 사용할 시 각각의 가설에 대한 기각역과 유의확률을 구하는 엑셀 함수는 다음과 같습니다.


이 엑셀함수를 예제에 적용해보겠습니다.
특정 제품에 대한 만족도 데이터이며 모평균의 점수가 65점보다 높다고 할 수 있는지에 대한 가설을 검정한 결과입니다.
귀무가설과 대립가설은 다음과 같은 좌측 검정입니다.

-표본 수 COUNT(데이터 범위) = COUNT(A2:A65) = 64
-표본평균 AVERAGE(데이터범위) = AVERAGE(A2:A65) = 70.34
-표준편차 STDEV(데이터범위) = STDEV(A2:A65) = 17.97
[설명] 먼저 표본수를 파악하기 위해서 COUNT(데이터 범위) = COUNT(A2:A65) = 64개의 표본을 조사했음을 알 수 있습니다.
다음은 표본평균을 구하기 위하여 AVERAGE(데이터범위) = AVERAGE(A2:A65) = 70.34임을 알 수 있습니다.
다음은 표준편차를 구하기 위하여 STDEV(데이터범위) = STDEV(A2:A65) = 17.97로 나타났습니다.
이제 검정통계량 값을 구하기 위하여 먼저 분자인 (표본평균 – 가설검정값) = 70.34 – 65 = 5.34 이며 검정통계량의 분모인 (표준편차 / 표본수의 제곱근) = (17.97/(64)½) = 2.246 임을 알 수 있으며 따라서 검정 통계량 T0 = 5.34/2.246 = 2.3788을 구할 수 있습니다.
우측검정의 기각역: T0 > =tinv(2α,n-1)
tinv(2α,n-1) = tinv(2X0.05, 64-1) = 1.669
[설명]위에서 우측검정의 기각역은 T0 > =tinv(2α,n-1) 라고 설명했습니다.
따라서 tinv(2α,n-1) = tinv(2X0.05, 64-1) = 1.669로 나타났습니다.
[중요] 검정통계량 값 T0 = 2.3788 > 기각치 = 1.669로 기각역에 해당함으로 귀무가설을 기각할 수 있습니다.
즉, 표본의 평균은 70.34이며 실제 모집단의 평균 점수도 65점보다 크다고 판단할 수있습니다.
또한 우측검정의 유의확률은 tdist(T0, n-1, 1) = tdist(2.3788, 64-1, 1) = 0.0102 < 유의수준 0.05이므로 귀무가설을 기각할 수 있습니다.
이와 같이 엑셀함수를 이용하여 검정통계량값과 기각역, 유의확률을 차례대로 구하여 귀무가설 기각 여부를 판단하면 됩니다.

분석도구로 t-검정
이제 두 번째 방법으로 메뉴탭에서 데이터 분석 → ‘t-검정 : 쌍체비교’를 선택해서 처리하는 방법을 설명하도록 하겠습니다.
먼저 측정 데이터가 있는 A열 옆 B열에 귀무가설 평균값인 65를 모두 입력합니다.
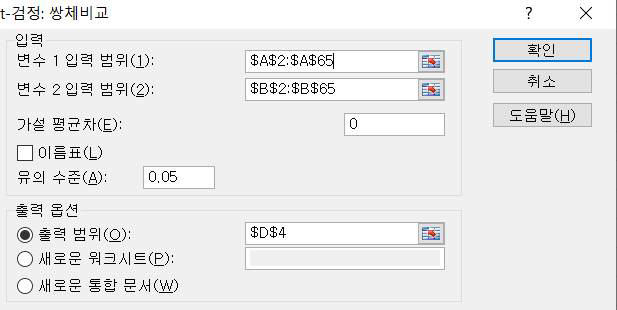
다음은 데이터분석 메뉴에서 ‘t-검정 : 쌍체비교’를 선택하면 다음과 같은 그림이 나타납니다.
1. ‘변수1 입력 범위’에 측정 데이터가 입력되어 있는 범위 (A2:A55)를 입력합니다.
2. ‘변수2 입력범위’에 귀무가설 평균값인 65가 입력되어 있는 (B2:B65)를 입력합니다.
3. 가설평균차에 ‘0’을 입력합니다. 1. 95% 신뢰수준이기 때문에 1-0.95 값인 0.05를 입력합니다.
4. 출력범위는 디폴트가 새로운 워크시트로 설정되어 있는데 이는 옆에 새로운 시트를 생성시켜 출력물을 제시합니다. 같은 화면에서 출력물을 보기위해 D4셀을 설정합니다
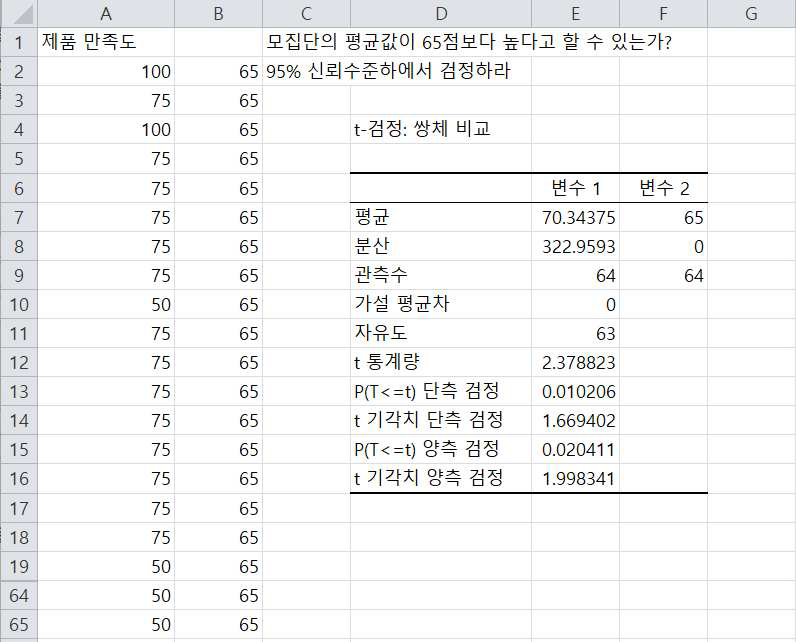
이제 확인을 클릭하면 다음과 같이 결과물이 제시됩니다.
표본 평균과 분산, 표본수 등의 기초 통계량 값과
t 통계량 = 2.3788
단측검정의 유의확률 = 0.0102
단측검정의 기각치 = 1.6694
로 앞에서 엑셀함수식을 이용하여 구한 값과 동일하게 나타남을 볼 수 있습니다.
분석 도구로 t-검정하는 경우 단측검정이 좌측검정인지, 우측검정인지 지정하지 않았기때문에 분석결과로 나온 단측검정 유의확률을 그대로 사용하면 안 됩니다. 만약 변수1의 평균이 평균2의 평균보다 크다는 가설검정을 하는데 t 통계량이 음수이면 단측검정의 유의확률은 1에서 표시된 값을 뺀 값을 사용해야 합니다. 마찬가지로 변수1 평균이 변수2 평균보다 작다는 가설검정에서 t 통계값이 양수이면 1에서 표시된 유의확률을 뺀 값이 해당 검정의 유의확률 즉 p값이 됩니다,
엑셀함수식을 이용하여 계산하는 방법보다 데이터 분석 → ‘t-검정 : 쌍체비교’를 선택해서 처리하는 방법이 훨씬 수월합니다.
독립표본 두 집단의 평균 t-검정
서로 다른 두 집단 간 평균 차이에 대한 유의성을 검정할 때의 방법 독립표본 t-검정을 하는 경우
- 자사와 경쟁사의 고객만족도 점수 차이
- 신제품과 기존제품에 대한 소비자 선호도 평가 점수 차이
- A브랜드와 B브랜드의 선호도 점수 차이
- 직원들의 상반기와 하반기의 직장 만족도 점수 차이
- 특정 약물의 투여 전후 치료 효과 차이
[설명]자사와 경쟁사의 고객만족도 점수 차이, 신제품과 기존제품에 대한 소비자 선호도 평가 점수 차이, A브랜드와 B브랜드의 선호도 점수 차이, 직원들의 상반기와 하반기의 직장 만족도 점수 차이, 특정 약물의 투여 전후 치료 효과 차 등 두 집단 간 평균 차이에 대한 유의성을 검정할 때 역시 T-검정 방법을 사용합니다.
두 집단 간 평균차이 검정을 수행하는 가설과 기각역은 다음과 같은 형태로 설정할 수 있습니다.
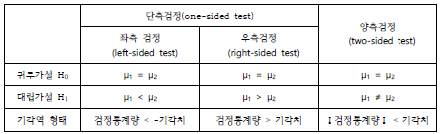
두 집단 간 평균 차이 검정은 독립표본의 평균차이 검정과 대응표본의 평균차이 검정으로 나눌 수 있습니다.
독립표본의 평균차이 검정은 두 표본의 데이터가 서로 독립인 경우이며 예들 들면 경쟁사와 자사의 고객들에게 각각 고객만족도 조사를 진행하여 얻은 데이터는 서로 아무런 영향을 미치지 않는 독립적인 데이터일 것입니다.
반대로, 동일한 응답자 집단에게 2개 브랜드의 음료제품에 대한 맛-테스트를 진행하였다면 응답자의 특성에 의한 편향이 개입되므로 첫 번째 제품에 대한 평가와 두 번째 제품에 대한 평가가 서로 독립적일 수 없을 것입니다. 이러한 표본을 대응표본이라고 하며 대응표본의 평균차이 검정을 쌍체비교(대응비교) T-검정이라고 합니다.
독립표본의 평균차이 검정은 2집단의 모분산이 동일할 경우와 모분산이 다를 경우의 2가지가 있는데 전자를 ‘등분산 가정 T-검정’이라고 하고 후자를 ‘이분산 가정 T-검정’ 이라고 합니다.
따라서 2개의 집단이 독립표본일 경우 먼저 모집단의 분산이 동일한가에 대한 검정을수행해야 하는 데 이와 같은 모집단의 등분산성에 대한 확인은 F-검정을 통해서 판단합니다.
정리하면
1) 먼저 2개의 데이터셋이 독립표본인지 대응표본인지 확인하고
2) 대응표본일 경우는 쌍체비교를 진행
3) 독립표본일 경우는 등분산성 가설검정(F-검정)을 수행하여
4) F-검정 결과 확인된 등분산성 여부에 따라 ‘등분산 가정 T-검정’ 또는 ‘이분산 가정 T-검정’을 선택하여 수행합니다.
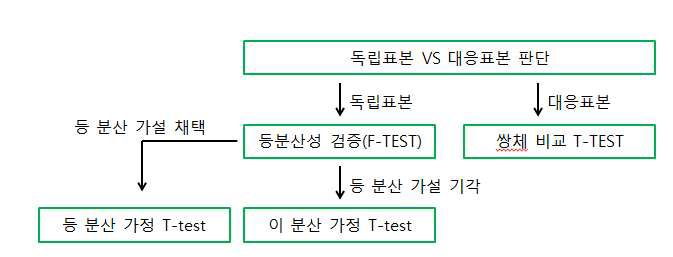
독립표본의 평균차이 검정에 대한 검정통계량과 기각역, 유의확률을 구하는 엑셀함수는 다음과 같습니다. 그러나 독립표본 t-검정에서는 데이터 분석 메뉴를 선택해서 얻을 수 있습니다.
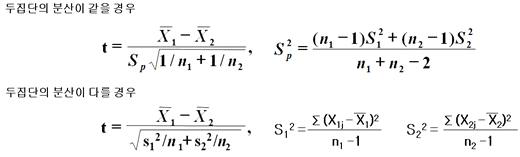
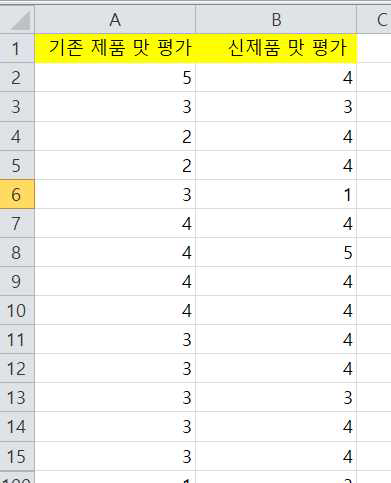
다음은 기존 제품과 신제품에 대한 평가를 각각 100명에게 받은 데이터입니다.
기존제품보다 신제품의 소비자 반응이 더 좋은지를 확인하고자 하며 95% 신뢰수준 하에서 검정하고자 합니다.
귀무가설과 대립가설이 다음과 같은 좌측검정이 됩니다.

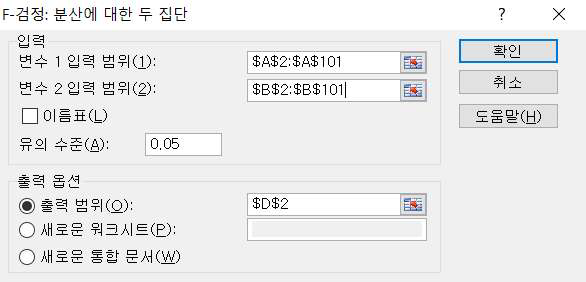
먼저 독립표본이므로 등분산성을 확인하기 위한 F-검정을 실시하기 위해서 데이터 분석 → ‘F-검정 : 분산에 대한 두집단’을 선택하면 다음과 같은 대화창이 나타납니다.
변수1의 입력범위에 기존제품의 평가 데이터 범위, 변수2의 입력범위에 신제품의 평가 데이터 범위를 입력하고 유의수준을 0.05로 설정한 후 출력범위를 지정한 후 확인을 클릭하면 출력물이 나타납니다.
두 집단의 등분산성을 검정하는 귀무가설과 대립가설은 다음과 같습니다.

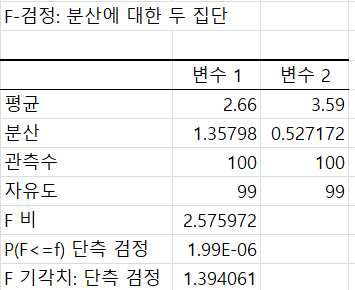
다음 출력물에서 보는 것과 같이 2개 데이터 집단의 기초통계량과 함께 F-검정 통계량과 유의확률, 기각치가 제시됩니다.
F-검정 통계량이 2.57 > 기각치 1.39 이므로 귀무가설을 기각합니다.
또한 유의확률이 1.99E-06으로서 < 0.05 이므로 귀무가설을 기각할 수 있습니다.
참고로 엑셀에서 ‘1.99E-06’은 1.99 X 10-6을 의미합니다. 지수로 표시된 숫자는 ‘Ctrl+Shift+~’ 단축키를 사용하면 일반 숫자로 표시할 수 있습니다. 단측 검정값 ‘1.88E-06’가 입력된 셀에 이 단축키를 적용하면 ‘0.00000199’숫자로 변환됩니다
두 집단의 모분산이 동일하다는 귀무가설을 기각했으므로 이제 이분산가정 T-검정을 진행하도록 하겠습니다.
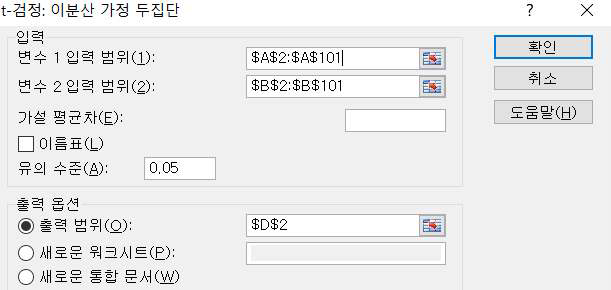
데이터분석 → ‘t-검정 : 이분산 가정 두 집단’을 차례로 선택하면 다음과 같은 대화창이 나타납니다.
변수1과 변수2의 입력범위에 각각 기존제품과 신제품의 평가 데이터 범위를 입력한 뒤 유의수준 0.05와 출력범위를 설정한 후 확인을 클릭하면 결과가 나타납니다.
기존제품과 신제품의 표본 평균이 각각 2.66, 3.59로 나타났으며 검정 통계량 값 –6.77 < 기각치 –1.655이고 유의확률이 1.04E-10 < 0.05 임으로 귀무가설을 기각하고 기존제품보다 신제품의 모평균 점수가 크다고 판단할 수 있습니다.
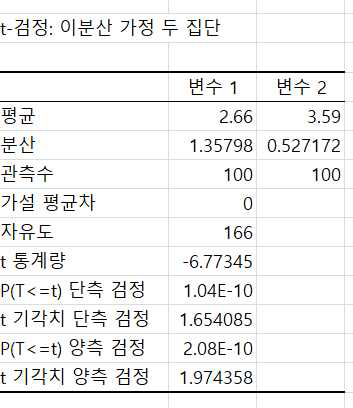
여기서도 주의해야 할 것은 변수1의 평균이 변수2의 평균보다 크다는 가설검정이었다면 t 통계량이 음수이기 때문에 실제 유의확률은 1에서 표시된 유의확률을 뺀 값으로 거의 1이고 귀무가설을 기각할 수 없습니다. 그러므로 분석도구를 이용한 t 검정에서 단측검정을 할 때는 대립가설과 t 통계량의 부호를 보고 해당 유의확률을 사용할 것인지 아니면 1에서 해당 확률을 뺀 값을 사용할지 결정해야 합니다.
대응표본의 두 집단의 평균 t-검정
대응표본의 쌍체비교 T-검정의 경우 귀무가설과 대립가설의 형태는 독립표본 T-검정과
동일하고 검정통계량과 유의확률, 기각역만 다른데 이 역시 엑셀의 데이터분석 → t-검
정 : 쌍체비교를 선택하면 결과물을 모두 제시해 줍니다.
다음은 어느 학교의 전교생 중 100명의 표본을 추출하여 1학기와 2학기의 영어 성적을 측정한 데이터입니다. 1학기에 비하여 2학기의 성적이 향상되었다고 할 수 있는지 95% 신뢰수준 하에서 검정하고자 합니다.
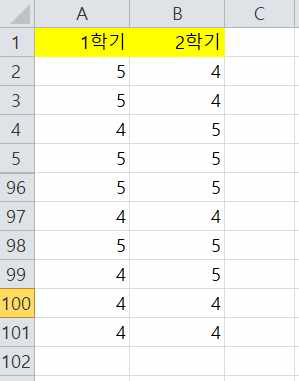
귀무가설과 대립가설이 다음과 같은 좌측검정이 됩니다.

데이터분석 → t-검정 : 쌍체비교를 선택하면 대화창이 나타납니다.
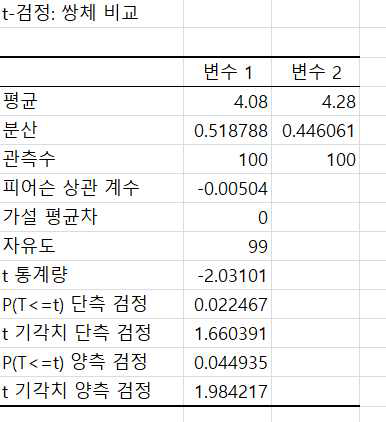
1학기와 2학기의 성적 데이터를 각각 입력하고 유의수준과 출력범위를 설정한 후 확인을 클릭하면 다음과 같이 결과가 나타납니다.
1학기와 2학기의 평균 점수가 각각 4.08, 4.28이고 또한 검정 통계량 –2.03 < 기각치 –1.66이고 유의확률이 0.02 < 0.05 임으로 귀무가설을 기각할 수 있습니다.
즉, 1학기에 비하여 2학기의 전체 학생들 영어 점수가 통계적으로 유의미하게 향상되었다고 판단할 수 있습니다.
'빅데이터 > 엑셀로 배우는 통계분석' 카테고리의 다른 글
| 이원 분산분석 (0) | 2023.06.02 |
|---|---|
| F-test (F-검정) (0) | 2023.06.01 |
| 가설 검정과 통계적 추정 (0) | 2023.05.31 |
| 통계 데이터의 시각화 방법 (0) | 2023.05.31 |
| 분산과 표준편차 (0) | 2023.05.30 |
- Total
- Today
- Yesterday
- 의료마이데이터
- 사이버공격 대응 전략
- 가트너 2023 전략기술
- 공격표면관리
- 5G
- IoT 안전 이용환경
- 리얼VR피싱
- 공격표면 관리 최소화 방안
- 마이헬스웨이
- lot 동향
- 디지털 휴먼 기술
- 공격표면 관리 개념
- 6G
- lot 센서 케이블 관리
- 사이버저
- 가트너 2023
- ls전선 전선관제
- 삼성 네 제로 홈
- 물류로봇 기술 동향
- 가트너 전략기술
- 지능형 IoT 보안
- 메타버스 대상
- IoT 보안 이슈
- 공격표면 관리 최신 동향
- 디지털 휴먼
- 아이튜버크리에이터
- IoT 보안 대응
- 디지털 휴먼의 발전 단계
- 물류로봇 시장 동향
- 디지털 휴먼 상호작용기술
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
