티스토리 뷰
산포도의 이해
- 산포도란 각 대푯값으로부터 데이터가 흩어져있는 정도입니다.
- 중심경향도를 확인함으로써 데이터의 대표적인 특징은 파악할 수 있으나, 데이터의 흩어진 정도를 알아야 실제 데이터를 제대로 이해할 수 있음
분포를 나타내는 값
분산, 표준편차, 범위, 사분위수, 백분위수
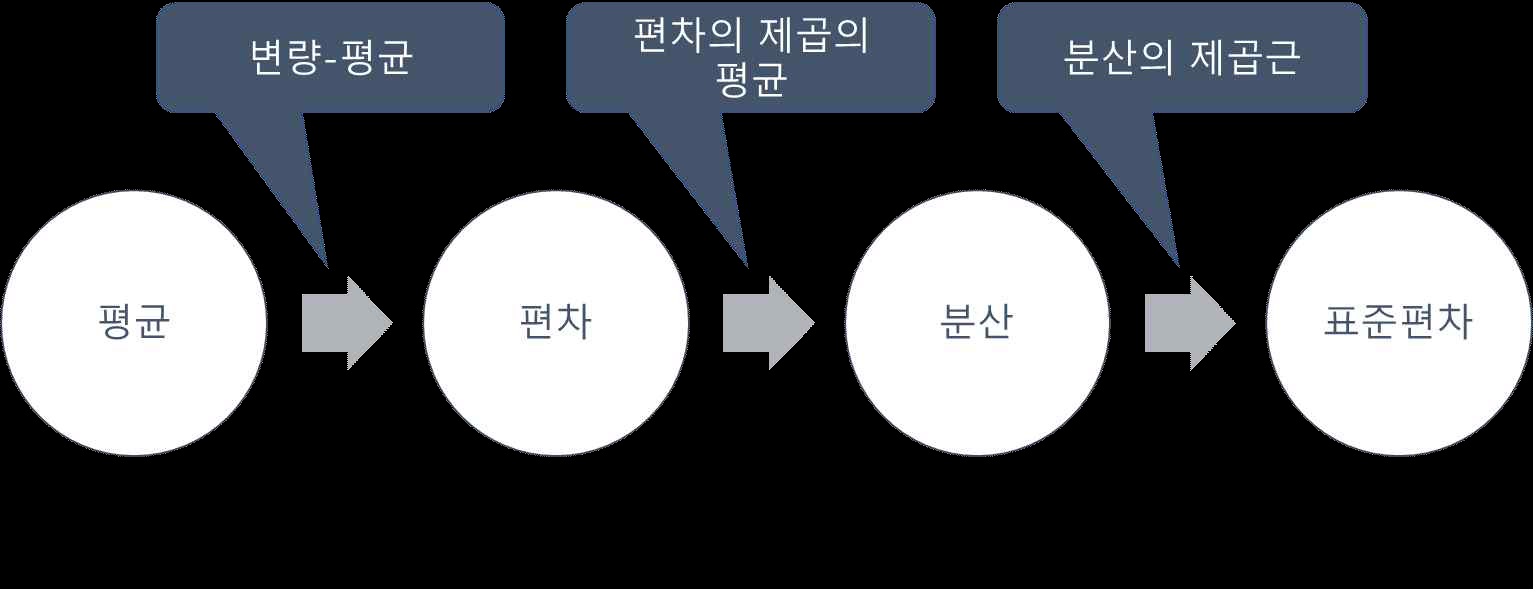
분산
데이터의 흩어진 정도를 표현하는 지표
데이터의 특성을 나타내는 대표적인 값은 평균이지만, 데이터의 분포를 표현하기는 어렵습니다다. 따라서 데이터의 분포를 확인해야 합니다.
데이터가 평균 가까이에 모여 있으면 왼쪽의 그림처럼 데이터의 분포를 표현할 수 있고, 평균에서 멀리 흩어져있는 데이터들의 형태는 오른쪽의 그래와 같은 모양을 같게 됩니다.

분산을 알기 위해서는 먼저 편차를 계산해야 하는데,
편차= 데이터의 값 - 평균값
편차의 합=0
편차는 평균값으로부터 떨어진 크기만큼 큰 값은 양수로, 작은 값은 음수로 계산되는데 이 편차의 합은 항상 ‘0’이다.
분산 = (편차)^2의 총합 / 데이터의 개수

편차를 제곱한 후 평균을 구한 값이 분산
분산은 그 자체로는 절대적인 의미를 갖지 않음. 단지, 산포의 크고 작음을 나타냅니다.
표준편차
표준편차= 분산의 제곱근
각 데이터들이 평균으로부터 떨어진 평균 거리
범위
데이터들의 최댓값과 최솟값의 차이
범위 값 자체가 데이터의 산포 정도를 보여주는 척도
사분위수
데이터를 오름차순으로 정렬한 상태에서 가장 작은 값으로부터
25%까지를 1사분위수
50%까지를 2사분위수
75%까지를 3사분위수에 해당하는 수
도표의 사분위수 위치를 사분위점이라 하고, 2사분위수는 중위수


백분위수
데이터를 크기가 작은 것부터 차례로 나열하여 가장 작은 값을 0으로, 가장 큰값을 100으로 하여 백분율로 특정 위치의 값을 표시
분포를 보여주는 그래프
데이터를 줄기와 잎으로 구분하여 데이터의 분포를 알아보는 방법

어떤 아파트 주민들의 나이를 정리할 때 나이 중 십의 자리를 왼쪽 줄기로, 일의 자리를 오른쪽 잎으로 구분하여 측정된 수치를 모두 나열해하면 각 줄기별로 각각의 변량을 모두 나타내면서도 각 각 줄기별 분포도 쉽게 파악할 수 있음
줄기와 잎 작성하는 방법
① 줄기와 잎 그림을 표현할 때는 가장 작은 수와 가장 큰 수를 파악하여줄기와 잎을 정한다.
② 세로선을 긋로 왼쪽에 줄기의 값을 쓰고, 오른쪽에 잎의 값을 크기가작은 값부터 모든 수치를 빠짐없이 쓴다.
③ 중복되는 값도 모두 작성하여 데이터의 분포와 양을 파악할 수 있게 한다.
분산과 표준편차의 계산

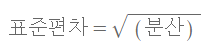
분산은 편차를 제곱하므로, 정확한 값을 표시할 수 없는 단점.
이 단점을 보완하려면 양의 제곱근을 구하면 되는데 이 값이 표준편차임.
분산과 표준편차는 데이터가 평균으로부터 가까이 있을수록 작아지고, 평균으로부터 멀리 떨어져 있을수록 커짐.
그러므로 분산과 표준편차의 값이 크다면 평균으로부터 차이가 커서 평균이 데이터의 값을 대표하기에 적합하지 않고, 분산과 표준편차의 값이 작다면 평균이 데이터를 대표하기에 적합하다고 판단할 수 있습니다.
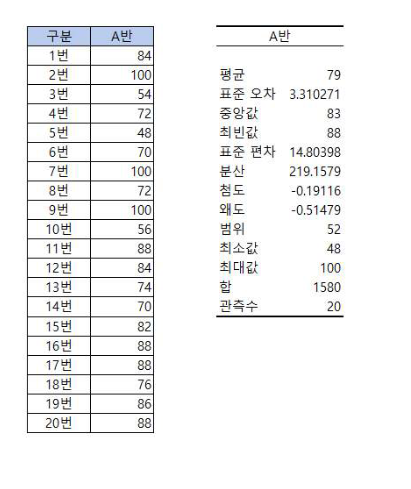
기술통계값 구하기
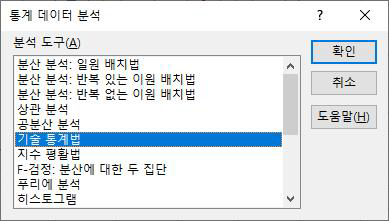
기술통계량은 수집된 데이터의 특징을 알 수 있는 대푯값 등을 요약하여 수치로 표시한 것
엑셀에서 기술통계량 구하는 방법
메뉴탭에서 [데이터]탭-[분석]그룹-[데이터 분석]명령을 클릭하여 필요한 분석도구를 선택
'빅데이터 > 엑셀로 배우는 통계분석' 카테고리의 다른 글
| 가설 검정과 통계적 추정 (0) | 2023.05.31 |
|---|---|
| 통계 데이터의 시각화 방법 (0) | 2023.05.31 |
| 중위수와 최빈수(대푯값) (0) | 2023.05.30 |
| 데이터 수집과 정리 (0) | 2023.05.29 |
| 엑셀 통계분석의 시작 (1) | 2023.05.29 |
- Total
- Today
- Yesterday
- 디지털 휴먼
- 디지털 휴먼 상호작용기술
- 리얼VR피싱
- 물류로봇 시장 동향
- IoT 보안 이슈
- 6G
- 디지털 휴먼의 발전 단계
- IoT 보안 대응
- 메타버스 대상
- 마이헬스웨이
- 의료마이데이터
- 아이튜버크리에이터
- ls전선 전선관제
- 공격표면 관리 최소화 방안
- 사이버저
- 사이버공격 대응 전략
- 공격표면관리
- 공격표면 관리 개념
- lot 동향
- 삼성 네 제로 홈
- 가트너 2023 전략기술
- 물류로봇 기술 동향
- 디지털 휴먼 기술
- lot 센서 케이블 관리
- 지능형 IoT 보안
- 공격표면 관리 최신 동향
- 가트너 전략기술
- 5G
- IoT 안전 이용환경
- 가트너 2023
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
