선형 회귀분석
회귀분석이란 한 변수가 다른 변수들에 의해서 어떻게 설명 또는 예측할 수 있는지를 알아보기 위해 적절한 함수식으로 분석하는 통계적 분석방법입니다.
이때 설명(예측)되는 변수를 종속변수(dependent variable) 또는 반응변수라 하고 종속변수를 설명(예측)하는 데 원인이 되는 변수를 독립변수(independent variable) 또는 독립변수라 합니다.

이러한 회귀분석은 자연과학은 물론 사회과학에서도 다양한 용도로 사용되고 있는데 독립변수와 종속변수 간 회귀 모형의 유효성, 독립변수에 의한 종속변수의 설명력, 특정 독립변수값에 대한 종속변수의 예측 등을 주로 분석합니다.
회귀분석은 모형의 선형성에 따라 선형회귀분석과 비선형회귀 분석으로 나눌 수 있는데 선형회귀분석은 종속변수와 독립변수의 관계가 선형함수로 표현할 수 있는 모형이며, 비선형 회귀분석은 종속변수와 독립변수의 관계가 선형이 아닌
비선형 관계에 적용하는 모형입니다. 여기서는 선형회귀모형에 대해서만 살펴보도록 하겠습니다.
또한 독립변수가 하나인 경우를 단순회귀(simple regression)분석이라 하고 독립변수가 2개 이상인 경우를 다중회귀(multiple regression)분석이라 합니다.
그럼 먼저 단순회귀모형에 대해서 살펴보도록 하겠습니다.
분석도구를 이용한 단순회귀분석
독립변수 X와 종속변수 Y의 단순회귀모형은 다음과 같은 식으로 표현될 수 있습니다.
Yi = β0 + β1xi + εi, i = 1, 2, 3, ... , n
Yi : 종속변수 Y의 i번째 관측치
xi : 독립변수 X의 i번째 관측치
β0 : 선형회귀함수의 절편
β1 : 선형회귀함수의 기울기
εi : i번째 오차항
n : 표본수
여기서 β0와 β1은 독립변수 X와 종속변수 Y의 관측치들로부터 추정하고자 하는 계수이며, εi는 오차항으로서 회귀모형에 포함된 독립변수 x 이외의 다른 요인들에 의해서 종속변수에 영향을 주는 요인이나 선형회귀모형의 함수적 형태에서 기인하는 오류, 종속변수를 측정할 때 발생할 수 있는 측정 오차 등을 포함합니다.
선형회귀모형에서는 기울기 β에 주로 관심을 갖는데 이는 독립변수 x가 1단위 증가할 때 종속변수 y의 평균 변화량을 나타냅니다.
즉, 회귀계수가 양수(+)로 추정되었다면 독립변수의 값이 증가할 때 종속변수의 값이 같이 증가하는 것이고, 회귀계수가 음수(-)로 추정되었다면 독립변수의 값이 증가할 때 종속변수의 값은 감소한다는 의미입니다.
한편, 이러한 회귀계수도 통계적 유의성이 없으면 의미가 없으므로 회귀계수의 유의성을 검정하여야 하는데 이에 대해서는 뒤에서 설명하도록 하겠습니다.
단순선형회귀 모형에서 β0와 β1를 구하는 기본적인 알고리즘은 이 오차항의 제곱을 최소화하는 β0와 β1를 추정하는 방식이며, 구체적 계산식은 선형대수와 미분방정식이 사용되는 데 여기서는 설명을 생략하도록 하겠습니다.
이는 엑셀의 데이터분석 도구에서 구할 수 있습니다.
또한 회귀모형이 성립되기 위해서는 오차항의 등분산성, 독립성, 정규성 등의 가정이 필요한 데 이를 확인하는 방법 또한 설명을 생략하도록 하겠습니다.
이제 예제를 통하여 단순회귀분석을 실행해 보도록 하겠습니다.
다음은 어떤 할인매장의 투입 판촉비 대비 매출증가분의 가상 데이터입니다.

먼저 독립변수(판촉비) 대비 종속변수(매출증가액)의 추세를 살펴보기 위해서 추세선을 한번 그려보겠습니다.
데이터 메뉴에서 ‘삽입’ → ‘차트’ → ‘분산형’ → ‘직선 및 표식이 있는 분산형’을 차례로 클릭하면 다음과 같은 데이터 분포 및 추세선이 나타납니다.
대략적으로 직선형의 증가 항수 형태가 나타남을 볼 수 있습니다.

다음은 구체적인 선형함수를 알아보기 위하여 차트 중 임의의 점(데이터위치)에 마우스를 올려놓고 오른쪽 마우스를 클릭한 뒤 ‘추세선 추가’를 선택하면 하면 추세선의 서식을 지정할 수 있는 메뉴가 나타납니다.

여기서 ‘선형’을 선택하고, 밑으로 가서 ‘수식을 차트에 표시’, ‘R-제곱 값을 차트에 표시‘를 선택하면 다음과 같이 함수식과 R-제곱값이 나타납니다.
종속변수 매출증가분과 독립변수인 판촉비의 선형함수는 y = 746751 + 30268x 이며 이는 판촉비가 백만 원 증가하면 매출이 30,268,000원 증가한다는 의미입니다.
또한 ‘R-제곱값’이 98.13으로 표시된 것의 의미는 매출액 증가분을 설명하는 데 있어서 판촉비가 98.1%를 설명한다고 해석할 수 있습니다.
이번에는 좀 더 자세한 결과를 도출하기 위하여 분석도구를 이용하여 분석해 보도록 하겠습니다.
분석도구에서 회귀분석을 선택하고 확인을 클릭하면 옵션을 선택할 수 있는 회귀분석 대화창이 나타납니다.
옵션 입력하는 대화창이 나타나면 Y축과 X축의 입력범위에 각각 종속변수와 독립변수의 데이터 범위를 입력합니다.
Y축 입력 범위 : 매출 증가
X축 입력 범위 : 판촉비
신뢰수준 : 95%
출력범위 : D2를 지정한 뒤 확인을 클릭하면 결과가 나타납니다.
출력물을 살펴보도록 하겠습니다.
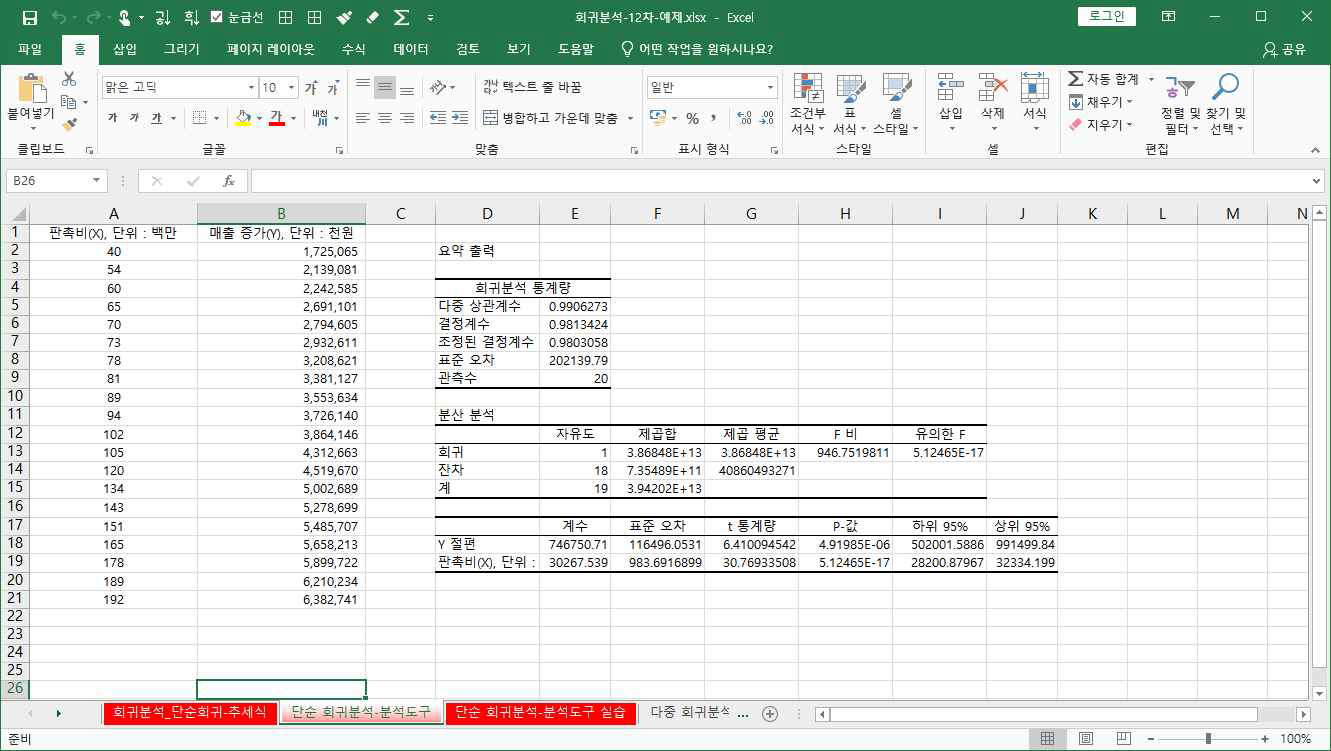
다중상관계수 : 0.9906273
종속변수의 관찰값과, 추정된 회귀모형에 의한 종속변수의 예측값 간 상관계수를 의미합니다.
0.990623이라는 통계량은 예측치와 실제 측정치 간 매우 높은 상관관계가 있음을 볼 수 있습니다.
결정계수 : 0.9813424
결정계수는 종속변수(매출증가분)는 다양하고 많은 요인들에 의해서 영향을 받을 수 있습니다. 이러한 다양한 요인들 중에서 독립변수(판촉비)가 설명하는 영향력의 비중을 의미합니다. 즉, 여기서는 판촉비가 매출증가분의 98.1%를 설명한다는 의미이며, 결정계수는 다중상관계수의 제곱과 동일하게 계산됩니다.
조정된 결정계수는 단순회귀모형에서는 의미가 없습니다.
다음은 회귀모형의 분산분석표가 제시되는데 추정된 회귀함수식의 유효성을 검정하는 데 사용됩니다.
종속변수의 전체 변동량을 회귀함수식에 의한 변동량과 오차항에 의한 변동량으로 나누어서 회귀함수에 의해 설명되는 변동량이 상대적으로 크면 회귀함수식이 유의하다고 판단하는 방식이며, 분산의 비인 F-검정통계량을 사용합니다.
여기서는 H13셀에 검정통계량 946.751이 주어졌고, I13셀에 유의확률 5.12E-17이 주어졌습니다. 유의확률이 0.05보다 작으므로 95% 신뢰수준 하에서 다음 귀무가설을 기각합니다. 즉 현재 회귀모형이 통계적으로 유의미하다고 판단할 수 있습니다.

한편, 엑셀도구를 이용한 분석에서는 검정통계량과 유의확률만 주어질 뿐 기각치는 주어지지 않는데 다음과 같은 엑셀함수로 유의확률과 기각치를 구할 수도 있습니다.
기각치 : =FINV(유의수준, 독립변수의 수, 표본수-독립변수의 수-1)
=FINV(0.05, 1, 20-1-1)
=4.414
유의확률 : =Fdist(검정통계량, 독립변수의 수, 표본수-독립변수의 수-1)
=Fdist(h13, 1, 20-1-1)
= 5.12465E-17
검정통계량 946.75 > 기각치 4.414이며 엑셀식에 의한 유의확률과 분석도구에 의한 유의확률이 동일함을 확인할 수 있습니다
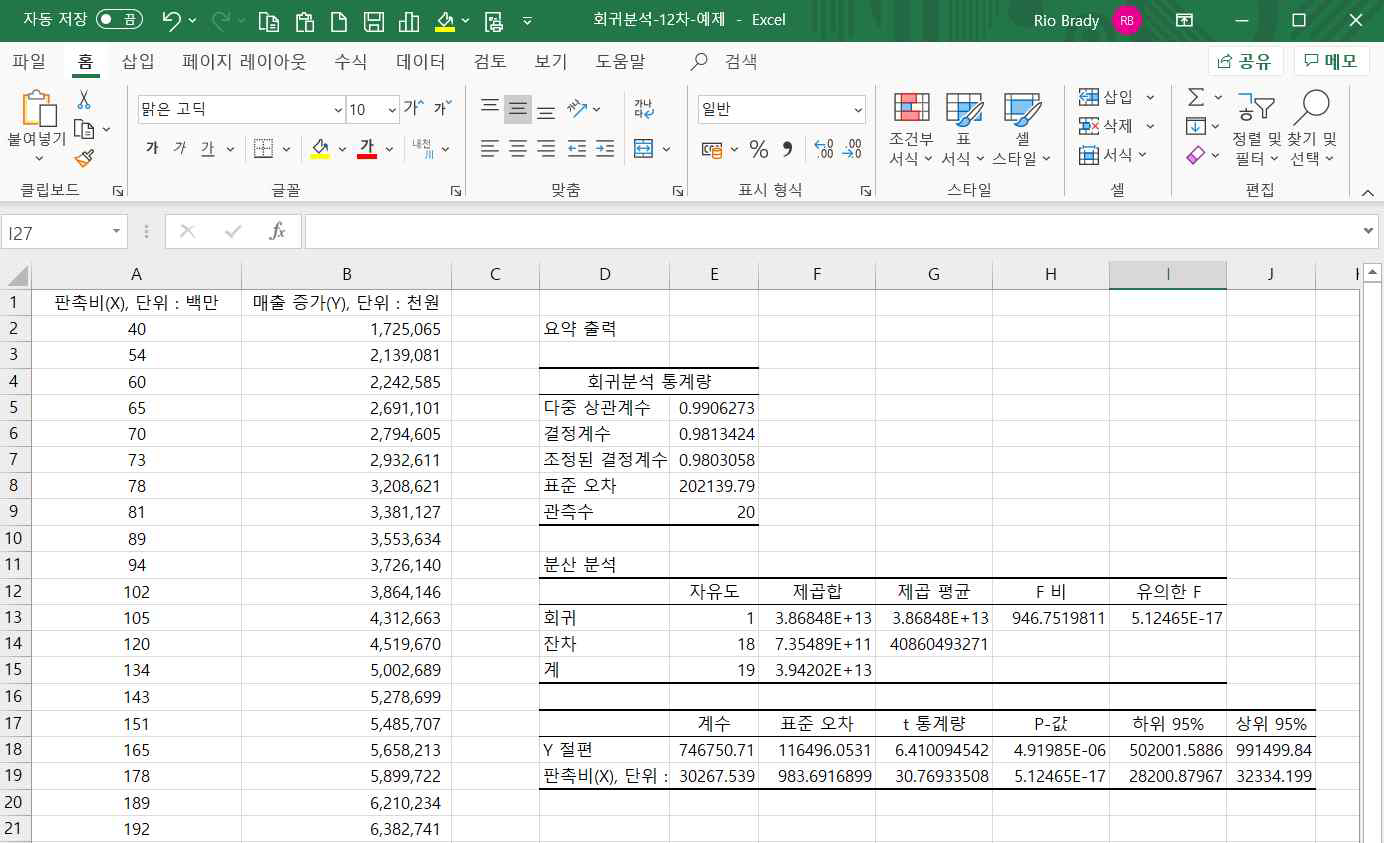
다음은 회귀계수에 대한 유의성을 검정한 결과가 제시되는 데 회귀분석에서 다음과 같은 회귀계수에 대한 유의성 검정은 t-검정 통계량을 사용합니다.

유의확률이 5.12465E-17 < 0.05이므로 귀무가설을 기각하고 회귀계수가 유의하다고 판단할 수 있습니다.
또한 양측검정의 기각치 =tinv(유의수준, 표본수-독립변수의 수-1) =tinv(0.05, 18)=2.1은 검정통계량 30.77보다 작으므로 귀무가설을 기각할 수 있습니다.
또한 앞서 추세식의 메뉴를 이용하여 추정한 함수식과 동일함을 볼 수 있습니다.
분석도구를 이용한 다중회귀분석
앞에서 판촉비라는 하나의 독립변수가 종속변수 매출액에 미치는 단순회귀모형에 대해서 살펴보았습니다.
그러나 실제로 종속변수는 하나의 요인이 아니라 2개 이상의 많은 변수들에 의해서 영향을 받는 것이 대부분일 것입니다.
또한 하나의 독립변수보다는 2개 이상의 변수들이 추가로 포함될 때마다 종속변수를 설명하는 회귀모형의 설명력이 높아질 것입니다.
이와 같이 2개 이상의 독립변수를 사용하여 종속변수를 설명하는 선형회귀모형을 다중 선형회귀분석이라고 합니다.
다중회귀모형은 다음과 같이 표현될 수 있습니다.
Yj = β0 + β1x1i + β2x2i +β3x3i + ...... + βpxpi +εi,
i = 1, 2, 3, ... , p j = 1, 2, 3, ... , n
Yj : 종속변수 Y의 j번째 관측치
xij : i번째 독립변수의 j번째 관측치
β0 : 선형회귀함수의 절편
βi : i번째 독립변수의 회귀계수
εj : j번째 오차항
p : 독립변수의 수
n : 표본수
이제 분석도구를 이용하여 단순회귀모형과 마찬가지로 모형의 통계적 유의미성을 확인하고 회귀계수에 대한 검정을 실시해 보도록 하겠습니다.
다음 예제는 어떤 은행 매장의 인테리어, 직원 친절성, 고객 편의시설, 주차편리성, 전반적 만족도에 대한 만족도 조사를 한 데이터입니다.
매장 인테리어, 직원친절성, 편의시설, 주차편리성을 독립변수로 하고, 전반적 만족도를 종속변수로 한 회귀분석을 실시해보도록 하겠습니다.
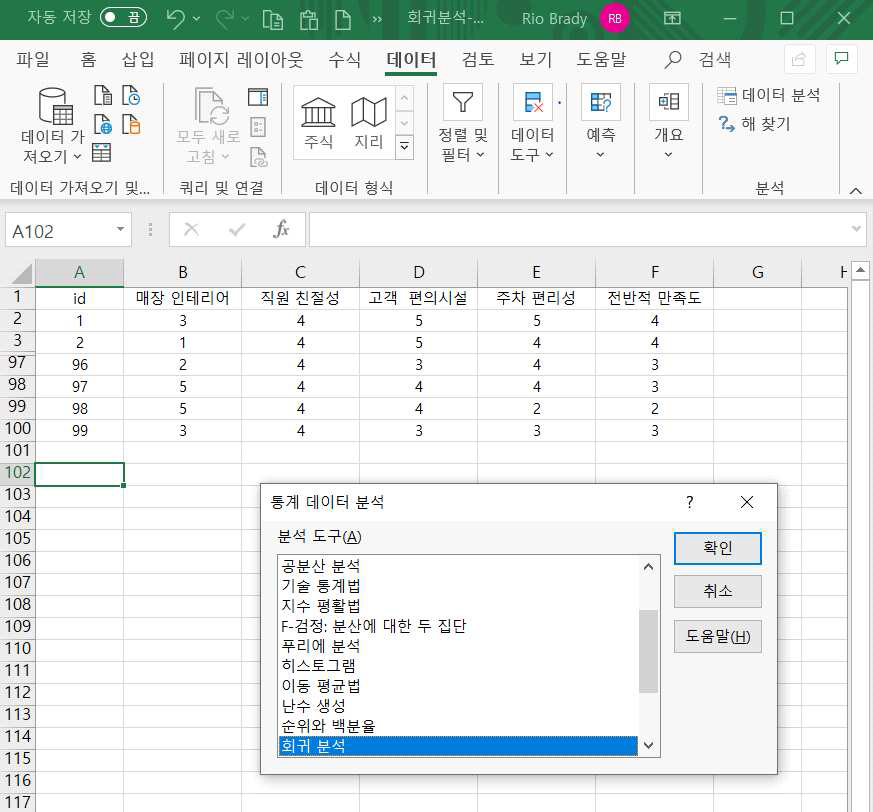
메인메뉴의 데이터 → 데이터분석 메뉴를 차례대로 클릭하면 다음과 같은 데이터 분석 도구가 나타납니다.
어기서 회귀분석을 선택하고 확인을 클릭하면 옵션을 입력하는 대화창이 나타납니다.
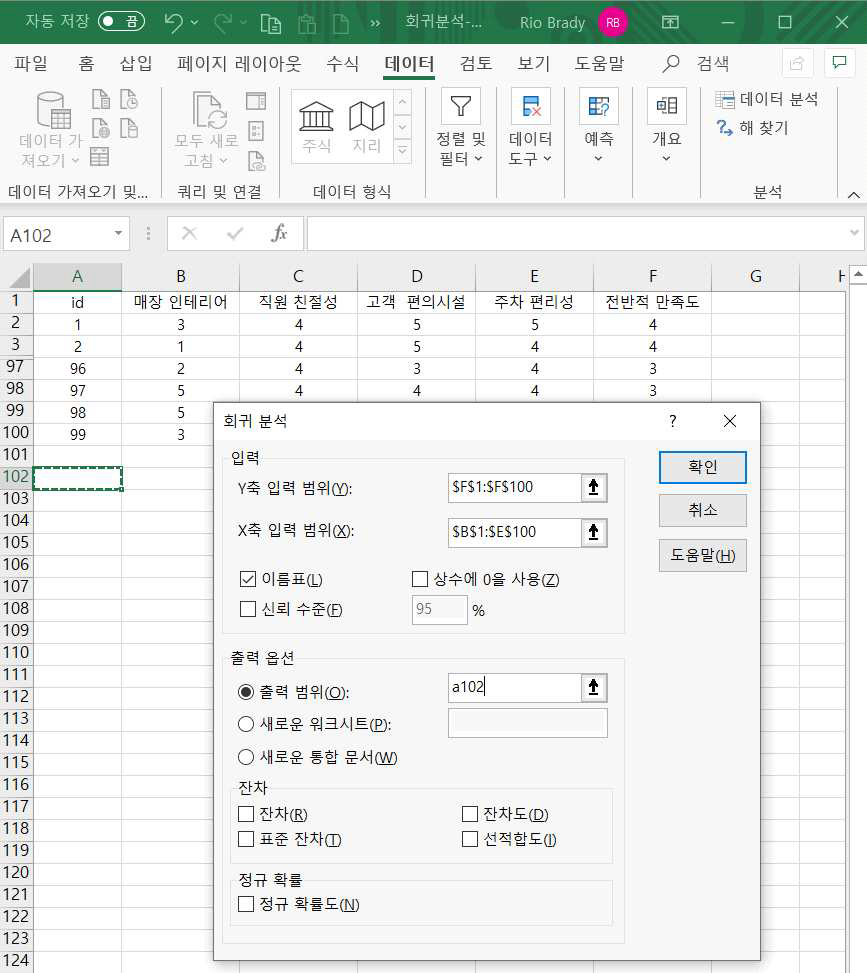
Y축의 입력범위에 전반적 만족도의 데이터범위인 F1:F100을 지정합니다.
X축의 입력범위에 독립변수들인 B1:E100을 지정합니다. 여기서 4개 독립변수들의 데이터 범위를 묶어서 하나의 영역으로 지정합니다.
다음은 이름표에 체크를 하는데 만약 위 데이터 범위을 입력할 때 한글 변수명을 제외 하고, 2행의 데이터 측정치부터 지정을 하였다면 이름표를 체크하지 않아야 합니다.
신뢰수준은 95%로 하는데 이는 연구자가 임의로 결정하는 것입니다.
출력범위를 지정하고 확인을 클릭하면 지정한 위치에 결과를 출력합니다.
먼저 회귀분석 통계량을 살펴보겠습니다.
앞에서 설명한 종속변수의 예측치와 실제치간 상관계수인 다중상관계수는 0.5121로서 낮지 않게 나타났습니다.
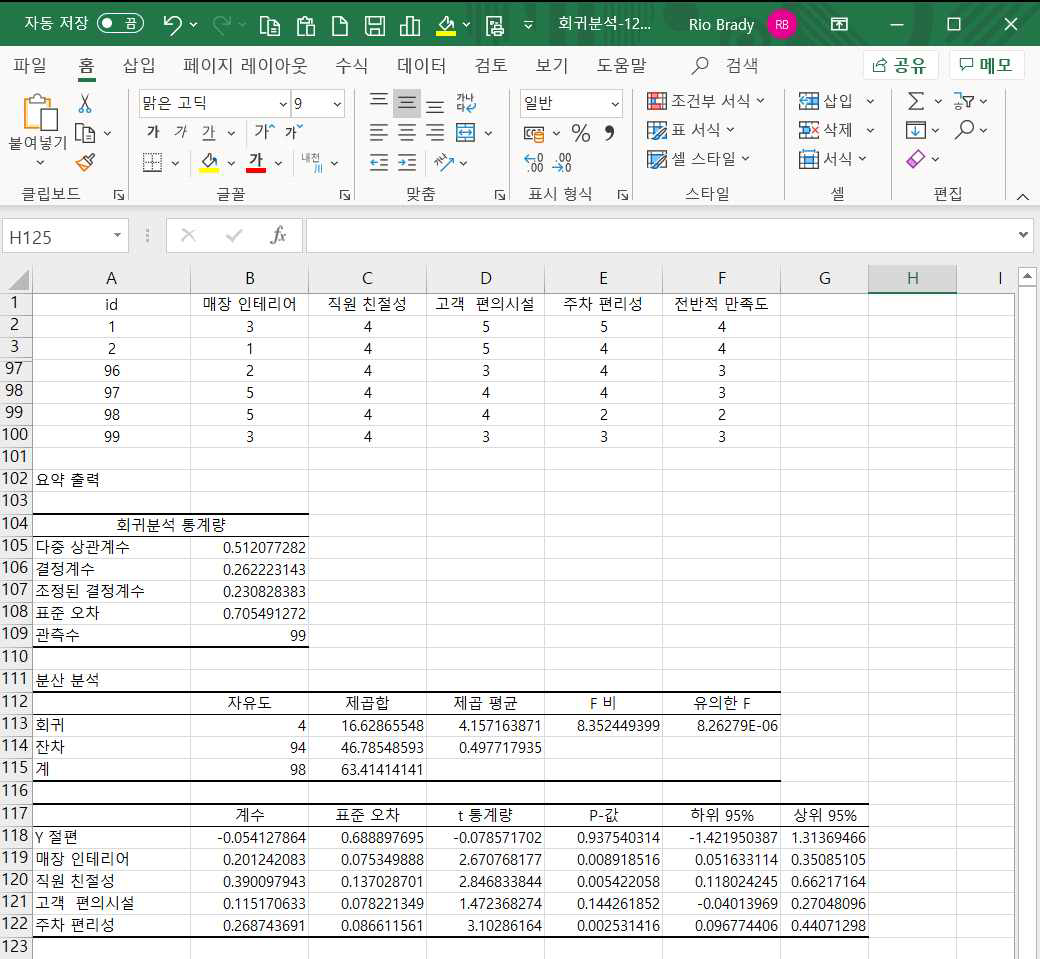
모형의 설명력인 결정계수는 26.22로 매장의 전반적 만족도를 설명하는데 현재 4개의 독립변수로 이루어진 회귀모형은 총 변동량의 26.22%를 설명하고 있습니다.
한편, 독립변수의 수가 많으면 많을수록 종속변수를 설명하는 영향력인 결정계수가 높아질 것입니다. 그렇다고 독립변수의 수를 무한정 많이 포함할 수도 없는 것입니다.
그래서 독립변수의 증감에 영향 받지 않는 순수 모델의 설명력을 의미하는 것이 조정된 결정계수입니다. 여기서는 23.1%로 나타났습니다.
그러면 ‘결정계수가 26.2% 밖에 안 되므로 4개의 독립변수에 의한 다중선형회귀모형이 의미가 없는가?‘ 하는 의구심이 들 수 있습니다.
그러나 그렇치는 않습니다.
이번에는 분산분석표를 살펴보도록 하겠습니다.
검정통계량이 8.35이고, 유의확률이 8.26E-06으로 유의수준 0.05보다 작으므로 귀무가설을 기각합니다.
참고로 다중선형회귀모형의 유의성을 확인하기 위한 가설을 다음과 같이 설정됩니다.
즉, 귀무가설이 모든 회귀계수가 0이라는 것이고 이는 곧 회귀모형 자체가
의미가 없다는 것을 의미합니다.

엑셀의 분석도구를 이용하여 회귀분석을 실행하면 검정통계량의 기각치를 제공하지 않습니다.
따라서 엑셀함수를 이용하여 기각치를 구해보도록 하겠습니다.
=finv(유의수준, 독립변수의 수, 표본수-독립변수의 수-1)
=finv(0.05, 4, 99-4-1)
=2.4685로서 검정통계량 8.35보다 작으므로 귀무가설을 기각할 수 있습니다.
즉, 앞에서 결정계수가 26.22%로서 본 회귀식이 전반적 만족도를 설명하는 정도는 낮지만 이는 4개의 독립변수 뿐 아니라 전반적 만족도에 영향을 미치는 다른 많은 요인들이 존재한다는 의미이지 현재 4개의 독립변수가 전반적 만족도에 무의미하다는 것은 아닙니다.
다음은 회귀계수들의 유의성에 대한 검정을 살펴보도록 하겠습니다.
4개 독립변수의 회귀계수에 대한 유의성 검정은 t-검정을 통해서 실시하며 각 통계량 및 유의확률이 제시되어 있습니다.
고객편의시설을 제외한 매장 인테리어, 직원친절성, 주차 편리성의 유의확률이 모두 유의수준인 0.05보다 작으므로 95% 신뢰수준에서 귀무가설을 기각할 수 있습니다.
즉, 고객 편의시설은 전반적 만족도에 유의미한 영향을 미치지 못하지만 나머지 3개의 만족도는 전반적 만족도에 영향을 미치고 있다고 볼 수 있습니다.
고객만족도 조사 데이터를 회귀분석 할 시 흔히 나타나는 다중공선성의 영향일수도 있습니다. 다중공선성에 대한 내용은 본 강좌의 수준을 벗어나므로 여기에서는 설명을 생략하겠습니다.
결정계수의 계산 및 이해
앞에서 언급한 것처럼 회귀분석은 전체 데이터의 변동량을 회귀모형식에 의한 변동과 오차에 의한 변동량으로 나누어서 오차제곱펑균(MSE) 대비 회귀제곱평균(MSR)이 크면 회귀모형식이 유의미하다고 판단하는 방식입니다.
이때 MSR/MSE가 F-검정 통계량으로 사용되는 것입니다.
한편, 전체 제곱합(TSS) 중에서 회귀식에 의한 회귀제곱합(SSR)이 차지하는 비중이 바로 R2값(결정계수)입니다.
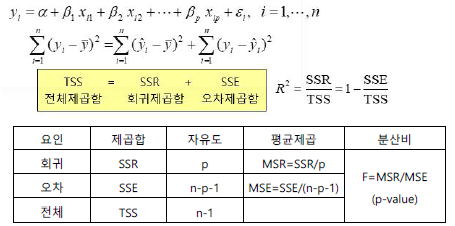
이 결정계수는 회귀식에 포함된 독립변수들이 종속변수를 어느 정도 설명할 수 있느냐에 대한 측도이지 모형 자체의 유의미성을 검정하는 측도는 아닌 것을 유의해야 합니다.
