χ2 (chi-square) 검정
교차분석과 χ2 검정 개념
교차분석이란 두 개의 범주형 변수 A와 B의 상호 관련성을 파악하고자 사용하는 분석방법으로 범주형 자료의 결합빈도를 작성하고 각 셀의 기대빈도를 구해 비교하여 두 변수 간 독립성 혹은 연관성이 있는지를 분석하는 방법입니다.
이때 두 변수 간 독립성 혹은 연관성 등을 검정하는 방법이 χ2(카이 스퀘어) 검정입니다.
두 개의 범주형 변수가 각각 p개와 k개의 범주를 가지고 있다면 교차표는 다음과 같은 형태를 나타냅니다.
p x k 교차표

이러한 교차분석표에 사용되는 검정 방법은 두 변수 간 독립성 검정과 비율의 동질성 검정, 관측빈도수와 예측빈도수의 비교를 통한 모형의 적합성 검정 등에 사용되며, 검정 통계량은 χ2(카이 스퀘어) 검정이 사용됩니다.
이중 적합도 검정은 본 강좌의 수준을 넘어가는 내용이므로 여기서는 두 변수간 독립성 검정과 균질성 검정에 대해서 살펴보겠습니다.
χ2 검정을 이용한 비율의 균질성 검정
2개의 행과 c개의 열로 이루어진 범주형 자료가 있는데 각 열의 2개 행이 서로 배반적인 사건으로 분류되어 있다고 가정하겠습니다.
예를 들면 성공과 실패, 남자와 여자, 만족과 불만족, 정상과 불량 등의 서로 배반적인(exclusive) 사건으로 분류된 범주형 자료가 있을 경우 집단 간(각 열 간) 행의 비율 즉 성공률, 남자 비율, 만족률, 불량률 등의 차이에 대한 검정을 하는 것을 범주형 자료의 비율차이 검정이라고 합니다.
이러한 2행 x c열의 데이터 구조는 다음과 같습니다.

※ nij : (i행, j열)의 빈도수
Cj : j열의 빈도수 합
Ri : I행의 빈도수 합
n : 전체 빈도수 합
이때 2개의 행이 서로 배반적인 사건으로 이루어져 있으므로 각 행과 열을 비율로 표시하면 다음과 같이 됩니다.

※ Pj = n1j / cj, j = 1, 2, 3, ..., C
C개 열의 비율차이에 대한 가설을 다음과 같이 설정됩니다.

그런데 엑셀의 데이터 분석도구에서는 이러한 비율 차이 검정에 대한 메뉴를 제공하지 않고 있습니다.
그래서 다소 번거롭지만 엑셀에서 제공하는 함수를 이용하여 비율 차이에 대한 검정을 수행해야 합니다.
먼저 2xc 교차표에 대한 예측치를 구해야 합니다. 즉, 각 셀에 대한 예측치를 구해야 하는데 (i행, j열)셀의 예측치는 (i행의 빈도수 합 x j열의 빈도수) / 총 빈도수로 계산합니다.

각 셀의 예측치를 구하려면 다음과 같이 계산을 해야 합니다.

예를 들어 1행1열 셀의 관측치(실제치) n11의 예측치 E11는 R1xC1/n, 2행 1열의 관찰치 n21의 예측치 E21 = R2xC1/n 과 같은 방식으로 구할 수 있습니다.
다소 번거롭고 반복적인 작업이지만 엑셀에서 $함수를 잘 이용하면 편리하게 작업을 할 수 있습니다.
같은 방식으로 모든 셀의 예측치를 다 계산하면 이제 검정통계량과 유의확률 기각치를 구해보도록 하겠습니다.
먼저 이러한 분할표의 chi-square 검정통계량은 다음과 같이 정의됩니다.

Oij : i행j열 셀의 관찰치
Eij : i행j열 셀의 예측치
즉, 모든 셀의 (관찰치 – 예측치)2 / 예측치의 합이 χ2 검정 통계량이 되며 엑셀에서 이러한 χ2 검정 통계량과 유의확률, 기각치는 다음과 같은 함수식으로 구할 수 있습니다.

이제 예제를 가지고 비율차이 검정을 해보도록 하겠습니다.
다음 데이터는 어떤 회사의 월요일부터 금요일까지 생산하는 제품의 불량률이 요일별로 차이가 있는지를 검정하기 위하여 각 요일별 100개씩 표본조사를 진행하여 얻은 정상제품 및 불량 제품의 빈도수입니다.

귀무가설 및 대립가설은 다음과 같이 설정됩니다.

먼저 각 셀의 예측치를 구하기 위하여 12행~13행과 같은 엑셀식을 입력합니다.
여기서는 B12~F13과 같은 엑셀식을 B17~F18위치에 입력하여 결과를 예측치 결과를 구했습니다.

이제 유의확률을 먼저 구해보도록 하겠습니다.
chi-square test에서 유의확률을 구하는 엑셀함수식은 =chitest(관측 도수 데이터 범위, 기대도수 데이터 범위)이므로
B22셀에 =CHITEST(B6:F7, B17:F18)을 입력하고 엔터를 치면 유의확률 0.0108이 나타납니다. 물론 꼭 B22셀이 아니라 결과를 출력하기 싶은 의미의 셀에 입력하면 됩니다.
다음 기각역을 구하는 엑셀 함수식은 =chiinv(유의수준, 자유도)이므로 B24셀에 =chiinv(0.05, 1x4)와 같이 입력하면 9.4877이 나타납니다.
마지막으로 검정통계량을 구하는 엑셀 함수식은 =chiinv(유의확률, 자유도) 이므로 B27셀에 =chiinv(b22, 1x4)을 입력하면
13.097이 나타납니다.
단, 여기서 자유도란 (행의수–1) x (열의수-1) 이므로 (2-1)x(5-1) = 4가 됩니다.
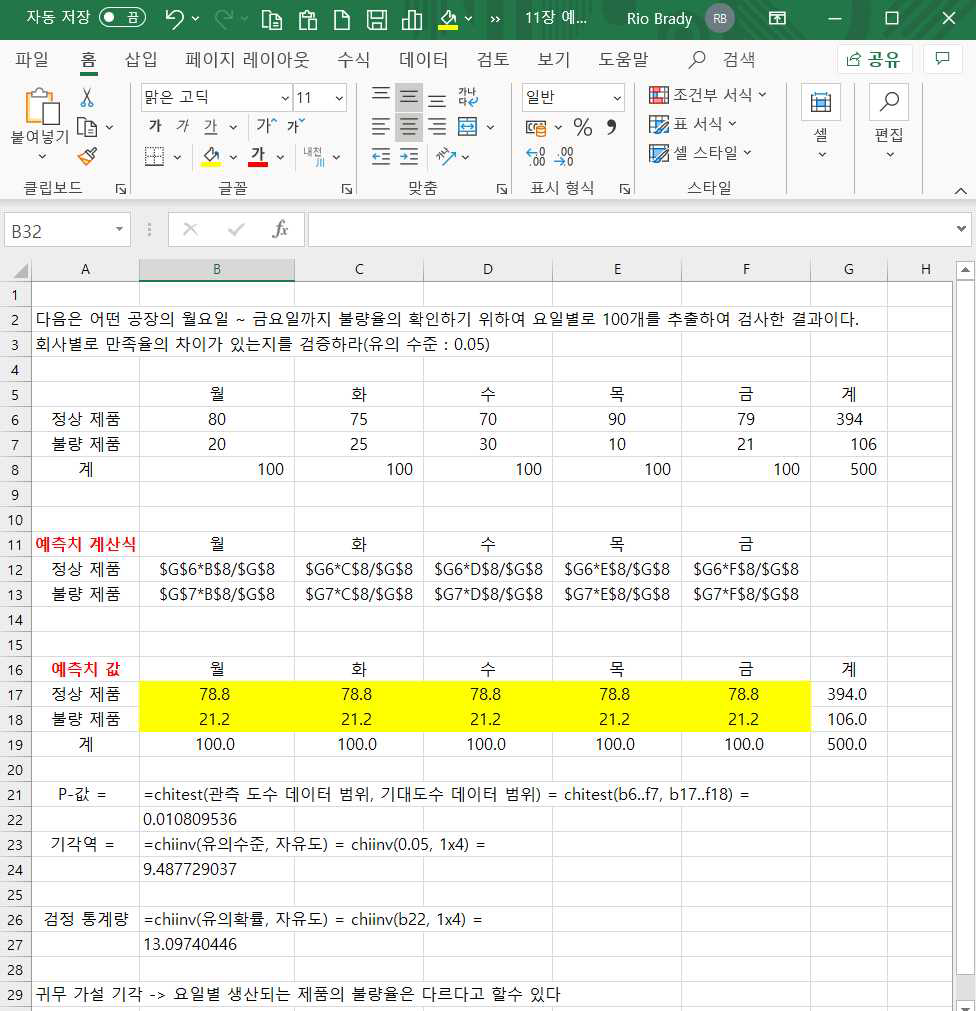
이제 검정 통계량 13.097 > 9.4877이고, 유의확률 0.0108 < 0.05 이므로 요일별로 불량률의 차이가 없다는 귀무가설을 기각할 수 있습니다.
χ2 검정을 이용한 비율의 독립성 검정
두 가지 속성이나 범주에 따라 빈도수로 분류한 범주형 자료에서 행과 열의 변수가 서로 연관성이 있는가 아니면 서로 연관성이 없는 독립의 관계인가를 검정하기 위해서도 chi-square test를 사용합니다.
이때 귀무가설과 대립가설은 다음과 같습니다.

한편, 범주형 자료에서 앞에서 설명한 비율의 균질성 검정과 두 변수의 독립성 검정의 통계량이 동일합니다. 따라서 앞에서 살펴본 비율의 균질성 검정 절차와 동일한 방식으로 독립성 검정을 진행하면 됩니다.
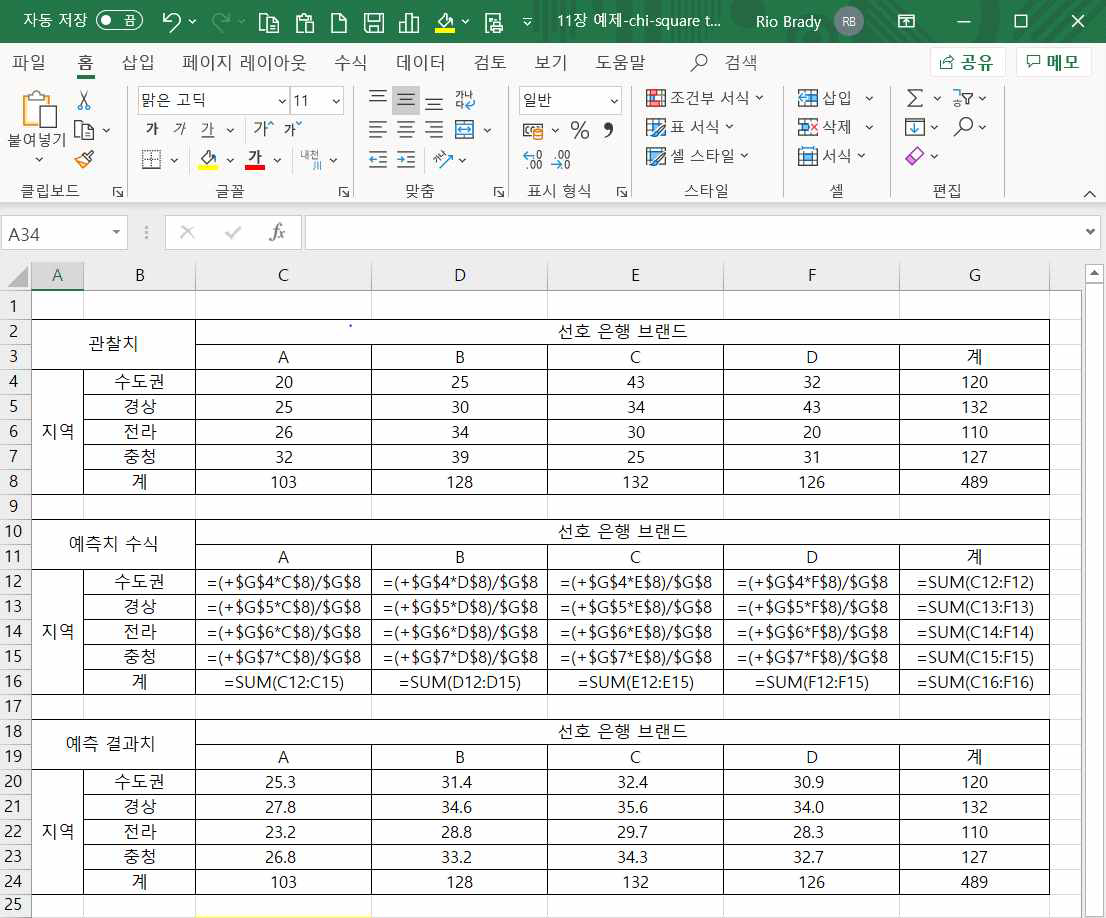
다음 예제는 각 지역별로 100명이 다소 넘는 사람들에게 국내 5개의 주요 은행 중 가장 좋아하는 은행 브랜드를 응답받은 데이터입니다.

응답자의 거주지역과 선호은행 브랜드 간에 연관관계가 있는지 아니면 서로 연관성이 없는 독립의 관계인지를 확인하고자 다음과 같이
가설을 설정하고 chi-square 검정을 실시해 보겠습니다. 단, 신뢰수준은 95%입니다.

앞의 비율 균질성 검정과 동일한 방식으로 검정통계량, 유의확률, 기각치를 구하기 위하여 먼저 각 셀의 예측치를 구해야 합니다.
앞에서 살펴본 것과 같이 각 셀의 예측치 ‘Eij = Ri x Cj / n’ 입니다.
따라서 ‘C12:G16’의 엑셀식을 ‘C20:G24’의 위치에 입력하여 각 셀의 예측치를 구하였습니다.
이제 유의확률을 구하기 위하여 =chitest(관측치 범위, 예측치 범위)인 =CHITEST(c4:f7,c20:f23)을 입력하여 0.0397을 구했습니다.
신뢰수준 95% 검정이므로 유의수준은 0.05입니다.
자유도는 (행의 수 –1)(열의수–1) = (4-1) (4-1) = 9입니다.
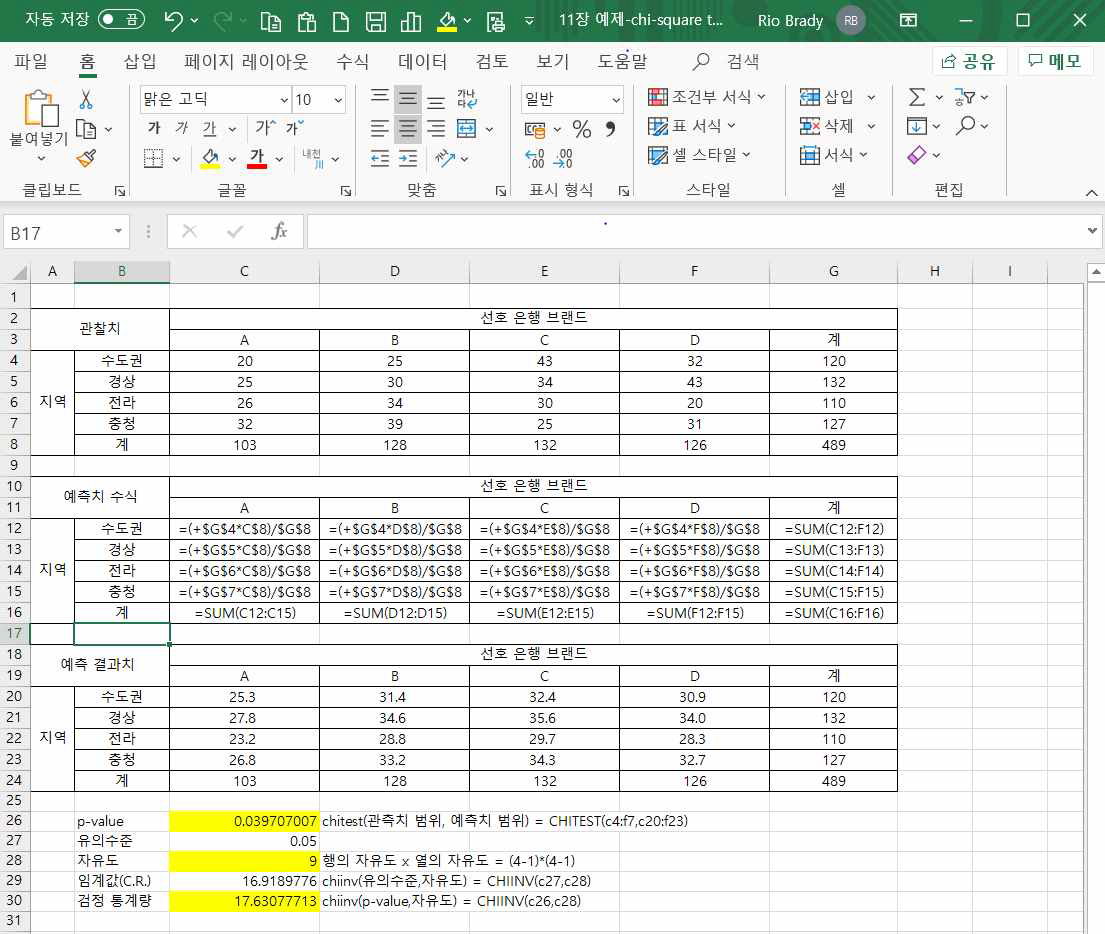
기각치를 구하는 엑셀함수식은 =chiinv(유의수준,자유도)이므로 = CHIINV(c27,c28)을 C29셀에 입력하여 16.919를 구했습니다.
검정 통계량을 구하는 엑셀함수식은 =chiinv(p-value,자유도)이므로 C30셀에 = CHIINV(c26,c28)을 입력하여 17.631을 구했습니다.
검정통계량 17.631 > 기각치 16.919이고, 유의확률은 0.0397 < 0.05이므로 귀무가설을 기각할 수 있습니다.
따라서 95% 신뢰수준 하에서 지역과 선호은행 브랜드는 통계적으로 유의한 연관관계가 있다고 결론 내릴 수 있다.
참고로 이와 같이 유의확률와 유의수준의 차이, 검정통계량과 기각치의 차이가 크지 않을 때
“95% 신뢰수준에서 귀무가설을 기각할 수 있지만 그 확률적 근거는 적은 편이다“ 라고 하는 것이 더 정확한 표현입니다.
