상관분석
상관분석의 개념
몸무게와 신장, 광고비와 매출, 알콜 섭취량과 혈압, 영어성적과 국어성적 등 서로 관련이 있을 것으로 예상되는 두 변수의 관찰값들이 쌍으로 주어졌을 때 두 변수간의 관계에 관심이 있다고 합시다.
이렇게 두 변수 간의 선형적인 연관성을 분석하는 것을 상관분석(correlation analysis)이라 하며, 두 연속형 변수들의 연관성을 측정하는 데 사용되는 통계치를 상관계수(correlation coefficient)라고 합니다.
상관계수는 칼 피어슨(Karl Pearson)에 의해 제안되었기 때문에 피어슨 상관계수라고도 합니다.
이러한 상관계수의 개념을 공부하기 전에 공분산(covariance)이라는 개념에 대해서 먼저 간략하게 살펴보겠습니다.
두 개의 확률변수 (X, Y)의 평균과 분산이 (μx, μy), (σx^2, σy^2)라고 하겠습니다.
공분산이란 확률변수 X가 증가함에 따른 확률변수 Y가 증가 또는 감소하는 경향의 정도를 측정하는 측도로서 (X-μx)(Y-μy)의 기대값으로 계산됩니다.

즉, 공분산이 큰 양의 값을 가진다는 것은 X가 증가할 때 Y도 증가하는 경향이 크다는 것이고, 공분산이 큰 음의 값을 가진다는 것을 X가 증가할 때 Y는 감소하는 경향이 크다는 것을 의미합니다. 또한 만약 공분산이 0에 가깝다면 확률변수 X, Y의 증감에는 서로 연관성이 거의 없다는 것을 의미합니다.
그런데 이러한 공분산은 측정 단위에 따라 달라지며 그 값의 범위가 제한되어 있지 않아서 두 변수 간 연관성의 정도를 비교하기가 어렵다는 한계가 있습니다.
예를 들면 다음과 같이 몸무게와 신장을 각각 kg과 m로 측정하여 공분산을 구하면 369.18이 되지만, 측정단위를 kg과 m가 아닌 g과 cm로 측정을 한다면 공분산이 35,918.3으로 엄청나게 커진다는 것입니다.
이와 같이 공분산은 실제 측정값이 동일하고, 두 변수 간 증가와 감소의 정도가 동일함에도 불구하고 측정단위가 바뀌면 공분산의 크기가 변화한다는 한계가 있습니다. 또한 공분산은 그 존재범위가 (-∞ ~ +∞) 무한하다는 특징도 있습니다.

이에 측정단위에 상관 없고 범위가 제한되어 있는 연관성의 측도가 상관계수인데 이는 공분산σxy를 각 확률변수의 표준편차로 나누어서 계산하며, 범위는 (-1 ≤ ~ ≤ +1)입니다.

앞에서 동일한 데이터임에도 불구하고 측정 단위가 달라짐에 따라 공분산이 크게 달라진 것에 비해 상관계수는 아래와 같이 동일함을 볼 수 있다.

이렇게 측정단위와 무관하게 두 변수의 선형적 관계 정도를 측정하는 계량적 지표를 상관계수라고 합니다.
한편 모집단인 두 변수의 상관계수를 모상관계수(population correlation coefficient, ρxy)라 하고, 표본으로부터 측정한 변수간 상관계수를 표본상관계수(sample correlation coefficient, rxy)라고 합니다.
산포도 유형별 상관계수
상관계수의 부호(즉 +, 1)는 크고 작음을 의미하는 것이 아니라 두 변수 사이의 증가나 감소의 관계를 나타내는 것입니다.
즉, 다음 그림에서 상관계수가 양(+)이라는 것은 변수 X가 증가할 때 Y도 감소한다는 것이고 상관계수의 부호가 음(-)이라는 것은 X값이 증가함에 따라 Y의 값은 감소한다는 것을 의미합니다. 이와 같이 두 변수의 값들을 좌표점으로 표시한 그림을 산점도(scatter plot)라고 하는데 자료의 대략적인 양상을 시각적으로 살펴보는 데 유용합니다.

또한 산점도를 보고 상관관계의 정도를 볼 수 있는데 상관계수의 값이 -1이나 +1에 가까우면(즉, 상관관계가 높으면) 산점도의 점들이 거의 직선 형태를 나타내고, 반대로 상관계수의 값이 거의 0에 가까우면(즉, 상관관계가 낮으면) 산점도의 점들이 무작위로 나타나거나 곡선의 형태를 나타냅니다.
즉, 아래 그림에서 왼쪽은 상관계수가 0.8로 직선의 주변에 데이터가 집중되는 정도가 80%임을 의미하고, 오른쪽은 상관계수가 1로서 직선의 주변에 데이터가 집중되는 정도가 100%이어서 직선위에 모든 자료들이 놓여 있음을 의미합니다.

한편, 상관계수가 0이라고 해서 무조건 두 변수 간의 아무런 관계가 없다고 해석해서는 안되는데 다음 그림에서 왼쪽의 경우는 상관계수가 0으로서 두변수간의 특정한 관계가 없음을 볼 수 있지만 오른쪽의 산점도는 두 변수 간 선형관계가 아닌
(비선형)곡선의 관계가 있음을 볼 수 있다.
이는 상관계수가 두 변수 간 선형적 관계를 나타내는 측도이기 때문이므로 상관계수가 0이라고 해서 두 변수는 아무런 상관관계가 없다고 판단해서는 안 됩니다.

만약 두 연속형 변수간의 산점도가 곡선이나 다른 비선형적인 관계를 나타내면 이에 부합하는 비선형 모형을 고려해야 합니다. 비선형 모형에 대한 자세한 내용은 본 강좌의 수준을 벗어나는 내용이므로 설명을 생략합니다.
상관계수 계산
엑셀을 이용해서 상관계수를 구하는 방법은 두 가지가 있는데, 첫 번째는 엑셀 함수를 이용하는 방법이고, 두 번째는 분석 도구의 상관분석이라는 메뉴를 이용하는 방법입니다.
엑셀 함수를 이용하는 방법
첫 번째 엑셀에서 상관계수를 구하는 명령어는 ‘=correl(x변수의 데이터 범위, y변수의 데이터 범위)‘입니다.
다음은 어느 커피숍의 커피맛에 대한 만족도와 인테리어에 대한 만족도, 그리고 해당 매장의 재방문의향을 질문하여 얻은 데이터입니다.
먼저 커피맛 만족도와 재방문의향 간 상관계수는 correl(커피맛 평가의 데이터 범위, 재방문의향 데이터 범위) =correl(b2:b51, d2:d51)을 입력하고 엔터를 치면 -0.0528이 나타납니다. 여기서는 b53셀에 입력을 하여 결과를 얻었습니다.
다음 인테리어 만족도와 재방문의향 상관계수는 correl(인테리어 만족도의 데이터 범위, 재방문의향 데이터 범위) =correl(c2:c51, d2:d51)을 b54셀에 입력하여 상관계수 0.0.63을 얻었습니다.

분석 도구의 상관분석 메뉴를 이용하는 방법
이제 엑셀의 데이터 분석 도구를 이용하여 구해보도록 하겠습니다.
메인화면에서 데이터 → 데이터 분석 메뉴를 차례대로 클릭하면 ‘통계 데이터 분석’ 메뉴가 나타납니다.

상관분석 메뉴를 선택하고 확인을 클릭하면 옵션을 선택하는 대화창이 나타납니다.
입력범위에 데이터가 입력되어 있는 범위 b2:d51을 지정합니다. 엑셀의 상관분석 도구에서는 변수별로 데이터 범위를 따로 입력하는 것이 아니라 상관계수를 구하려는 모든 변수들의 데이터 범위를 묶어서 한 번에 지정합니다. 데이터 방향은 열을 선택합니다.
출력범위에는 분석 결과가 제시될 위치를 지정합니다. 여기서는 a56을 지정했습니다.
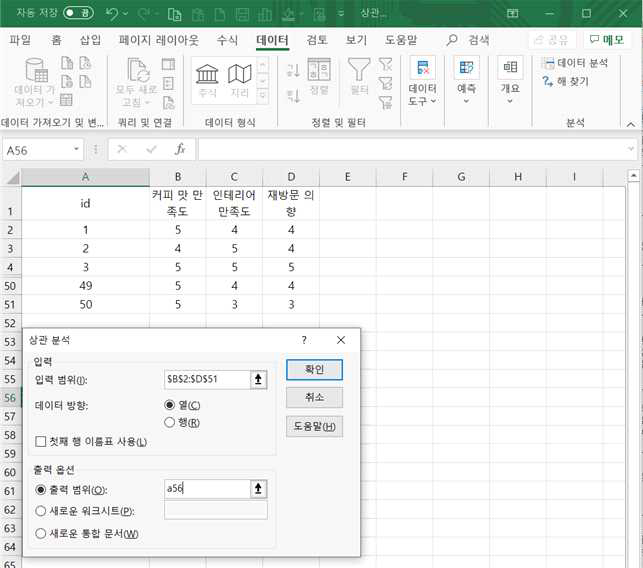
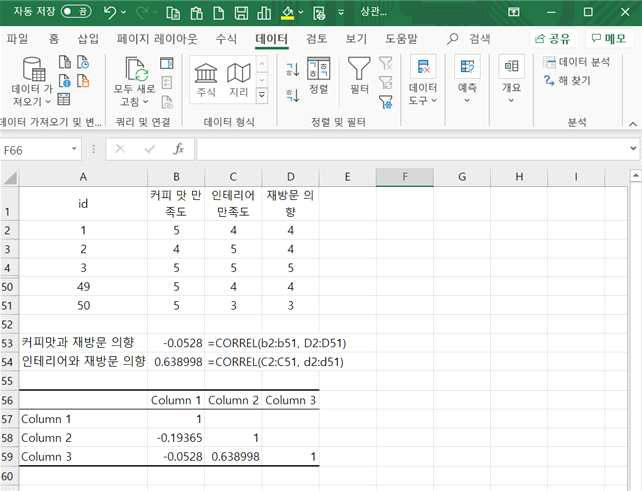
확인을 클릭하면 출력물이 나타납니다.
커피맛에 대한 만족도, 인테리어 만족도, 재방문의향을 각각 column1, column2, column3 으로 지정하여 상관계수가 출력되었습니다.
column1(커피맛 만족도)과 column3(재방문의향)의 상관계수 –0.0528, column2(인테리어 만족도)와 column3(재방문의향)의 상관계수 0.64가 나타났고 앞에서 엑셀 명령어 =correl 함수를 사용해서 구한 것과 동일함을 확인할 수 있습니다.
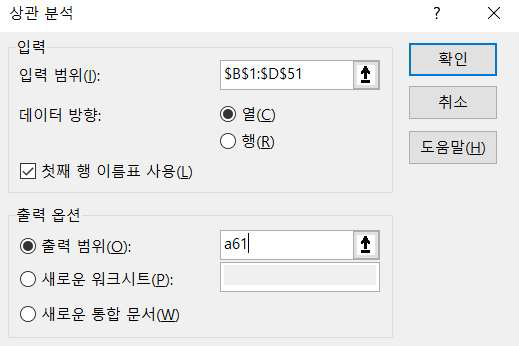
만약 앞에서 데이터 범위를 (b2:d51)이 아니라 (b1:d51)로 지정하고, ‘첫째 행 이름표 사용’을 선택하고 확인을 클릭하면 column1, column2, column3이 아니라 원래의 변수명 커피맛 만족도, 인테리어 만족도, 재방문의향으로 결과가 제시됩니다.
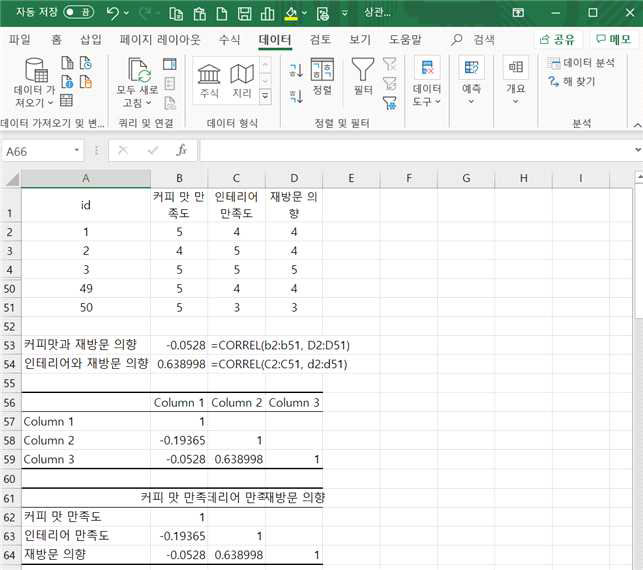
이와 같이 여러 변수들의 상관계수들을 행과 열로 정리된 것을 상관계수 행렬(correlation matrix)이라고도 합니다.
이러한 상관계수 행렬에서 대각선 윗부분이 공란으로 나타나는 것은 대각선 아래 부분과 대칭이기 때문입니다.
즉, 변수1과 변수3의 상관계수나 변수3과 변수1의 상관계수는 동일하기 때문에 대각선 아래 부분은 제시하고 있습니다.
통계에서 일반적으로 사용하는 척도의 종류
다음은 통계에서 일반적으로 사용하는 척도의 종류에 대해서 간단하게 살펴보도록 하겠습니다.
어떤 특정한 사건을 숫자로 전환하는 함수를 우리는 확률변수라고 합니다.
예를 들면 동전을 2번 던져서 나타날 앞면의 숫자를 확률변수 X라고 정의하면 2번 모두 앞면이 나오는 경우 확률변수 X의 값은 2, 앞면이 한번 뒷면이 한번 나오는 경우 확률변수 X의 값은 2, 앞면이 한 번도 나오지 않을 경우 확률변수 X의 값은 0이 되는 것입니다.
이러한 측정 변수는 4개의 척도로 나뉘는데 비율척도, 간격척도, 순서형척도, 명목형 척도가 있습니다.
비율척도란 비교가 가능한 간격척도의 특성을 포함하며, 값간 간격이 동일하고 비율 계산이 가능한 척도로서 길이, 무게, 시간, 나이 등이 해당됩니다.
간격척도란 값간 간격이 고정된 척도로서 값간 차이에 의미가 있으며 값 간의 비율은 무의미하며, 온도 등이 해당됩니다.
순서형 척도란 명목형 척도의 성격을 가지고 있으며 크기 순서대로 서열화가 가능합니다. 값 간의 구체적인 차이는 나타내지 않고, 단지 순서만을 의미합니다.
예를 들면 학업 성적 등수, 키의 크기 순서 등이 해당됩니다.
명목형 척도란 속성을 숫자로 구별하기 위한 목적으로 사용됩니다.
숫자의 크기는 의미가 없고 단지 범주의 수준을 가리키는 것일 뿐입니다.
예를 들면 남자는 1, 여자는 2와 같은 방식으로 어떤 속성의 세부 수준을 가리키는 숫자일 뿐입니다.