이원 분산분석
이원 분산분석의 개념
일원분류 분산분석은 하나의 요인에 대한 여러 처리 수준의 평균차이에 대한 검정을하는 방법입니다.
그러나 특정 기업의 매출은 하나의 요인이 아니라 경쟁사 상황, 가격, 브랜드, 경제상황, 지역 등 다양한 요인에 의하여 영향을 받을 것입니다.
또는 특정 브랜드의 고객만족도 점수도 응답자의 거주 지역, 성별, 연령, 제조 회사 규모 등 다양한 요인에 의해 영향을 받을 수 있습니다.
이렇게 많은 요인들 중에서 관심이 있는 반응값(예를 들면 고객만족도)에 영향을 주는 두 개의 요인에 대한 영향을 알아보고자 할 때 사용하는 검정 방법이 이원분류 분산분석입니다.
이러한 이원분류 분산분석 방법에는 2개 요인의 각 수준별 조합에서 반복이 있는 경우와 반복이 없는 경우가 있습니다.
전자를 ‘반복측정 이원분산분석’ 이라고 하고 후자를 ‘반복 없는 이원분산분석’ 이라고 합니다.
먼저 ‘반복이 없는 이원분산분석’에 대해서 살펴보도록 하겠습니다.
반복 없는 이원분산분석
어떤 식품 회사가 편의점에서 판매되는 자사의 라면 점유율이 알고 싶어서 a개의 도시에서 b개의 점포규모별로 점유율을 추정해서 다음과 같은 자료를 얻었습니다.

이와 같은 자료에서 점유율에 영향을 주는 도시와 점포규모의 영향을 확인하고 싶을때 반복없는 이원분류 분산분석을 사용하며 이때 사용되는 모형은 다음과 같이 표현할 수 있습니다.
즉, i번째 점포규모와 j번째 도시의 점유율 yij는 총평균 μ, 요인 A(점포규모)의 i번째 처리(점포규모)의 효과, 두 번째 요인 B(도시)의 j번째 처리(도시)의 효과, 오차항으로 구성되어 나타납니다.

이러한 이원분류 분산분석에서는 2가지의 귀무가설과 대립가설이 설정될 수 있습니다.
첫째 점포 규모별 점유율 차이에 대한 가설은 다음과 같습니다.

둘째 도시별 점유율 차이에 대한 가설은 다음과 같습니다.

일원배치 분산분석에서는 전체 데이터의 변동을 처리제곱합과 잔차제곱합으로 나누어서 잔차제곱평균 대비 처리제곱평균이 크면 각 처리별 평균의 차이가 있는 것으로 판단하는 방식이었습니다.
이원분류 분산분석은 전체 변동(TSS)을 A요인의 처리제곱합(SSA), B요인의 처리제곱합(SSB), 잔차제곱합(SSE)으로 분할하고, 잔차제곱평균(MSE) 대비 A요인의 처리제곱평균(MSA)이 크면 A요인의 각 처리별 평균의 차이가 있는 것이며, 잔차제곱평균(MSE) 대비 B요인의 처리제곱평균(MSB)이 크면 B요인의 각 처리별 평균의 차이가 있는 것으로 판단합니다.
※ 반복이 없는 이원분류 분산분석표

즉, 검정통계량 Fa = MSA/MSE가 기각치보다 크면 A요인(점포규모)의 처리별 평균이 모두 같다는 귀무가설을 기각하고, Fb = MSB/MSE가 기각치보다 크면 B요인(도시)의 처리별 평균이 모두 같다는 귀무가설을 기각합니다.
※ 반복이 없는 이원분류 분산분석의 검정법

다음은 통신사의 고객만족도 조사를 진행하였는데, 전국을 5개 지역으로 나누어서 조사를 진행한 결과입니다.

다음과 같은 2개의 가설을 검정해보도록 하겠습니다. 단 신뢰수준 95% 하에서 검정하도록 하겠습니다.

엑셀에서는 이와 같은 반복 없는 이원 분산분석을 데이터분석 메뉴에서 실행할 수 있도록 제공하고 있습니다.
엑셀의 메인메뉴에서 데이터 → 데이터 분석을 누르면 다음과 같은 대화창이 나타납니다. ‘분산분석 : 반복 없는 이원 배치법’ 메뉴를 선택한 후 확인을 클릭하면 그 다음 대화창이 나타납니다.

입력범위에 현재 데이터가 있는 범위 ‘A2:E7’를 입력하고, 이름표에 체크합니다.
다음은 유의수준에 0.05를 기입하고, 출력옵션의 출력범위에 결과물을 제시할 원하는 위치를 입력합니다. 여기서는 a9셀을 지정하였습니다.

먼저, 행(지역)과 열(통신사)의 처리별 만족도의 합과 평균, 분산 등 기초통계량이 제시되었습니다. 지역별로는 경상과 충청 지역의 평균 점수가 상대적으로 높고, 강원 지역의 만족도 점수가 낮은 것으로 나타났습니다.
그러나 이러한 지역별 평균 만족도 점수의 차이가 통계적으로 유의한 것인지를 확인하고자 하는 것입니다.
통신사별로는 S통신사의 만족도 점수가 상대적으로 낮고, L통신과 T통신사가 비슷하게 1위를 점하고 있으며, R통신사가 중간 점수를 나타내고 있습니다. 그렇다면 역시 통신사별로 만족도의 점수 차이가 통계적으로 유의한 것인지를 검정하고자 합니다.
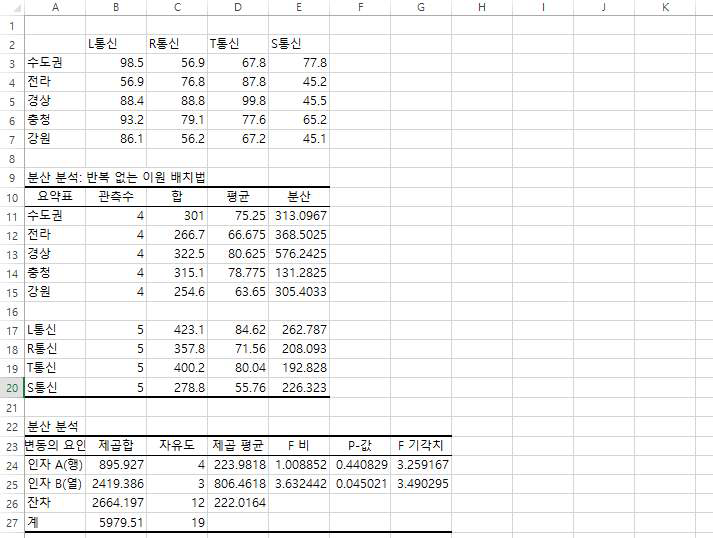
먼저 요인 A(행), 즉 지역별 만족도의 처리제곱 평균(MSA)은 223.982이고 잔차제곱평균(MSE)는 222.016입니다. 따라서 검정통계량 Fa= MSA/MSE= 1.009이고 이는 기각치 3.26보다 작습니다. 또한 유의확률 0.44는 유의수준 0.05보다 크므로
귀무가설을 기각하지 못합니다.
즉, 지역별로 만족도의 표본 평균 차이가 다소 나타나기는 했지만 95% 신뢰수준 하에서(지역별로 만족도 점수가 모두 동일하다는) 귀무가설을 기각하지 못하므로 통계적으로 유의한 점수 차이는 없다고 결론 지을 수 있습니다.
다음은 요인 B(열), 즉 통신사별로 만족도 점수의 차이에 대한 유의성을 살펴보겠습니다. 통신사별 만족도의 처리제곱평균(MSB)은 806.46이고 잔차제곱평균(MSE)은 222.016이므로 검정통계량 Fb = MSB/MSE = 3.63 으로서 F-기각치 3.49보다 약간 큽니다. 또한 유의확률은 0.045로서 유의수준 0.05보다 약간 작습니다.
따라서 귀무가설을 기각할 수 있습니다. 즉 통신사별로 만족도 점수는 차이가 있으며 이는 95% 신뢰수준 하에서 통계적으로 유의하다고 판단할 수 있습니다.
참고로 이렇게 검정통계량와 기각치, 유의확률과 유의수준의 차이가 작게 나타날 때는 “귀무가설을 기각할 수 있지만 그 확률적 근거는 매우 낮다“고 얘기하는 것이 더욱 정확한 표현입니다.
반복 있는 이원분산분석
다음 자료는 A, B, C, D 4개 은행의 고객만족도 조사를 진행한 자료입니다. 단 연령별로 각 30명씩 조사를 진행했습니다. 참고로 중간중간 측정 데이터를 숨기기 처리하였습니다. 이렇게 연령과 은행이라는 2개의 요인별로 측정을 하되 각 수준별로 반복하여 측정한 자료의 평균값 차이 검정을 하기 위해서는 ‘반복이 있는 이원 분산분석’을 이용하여야 합니다.
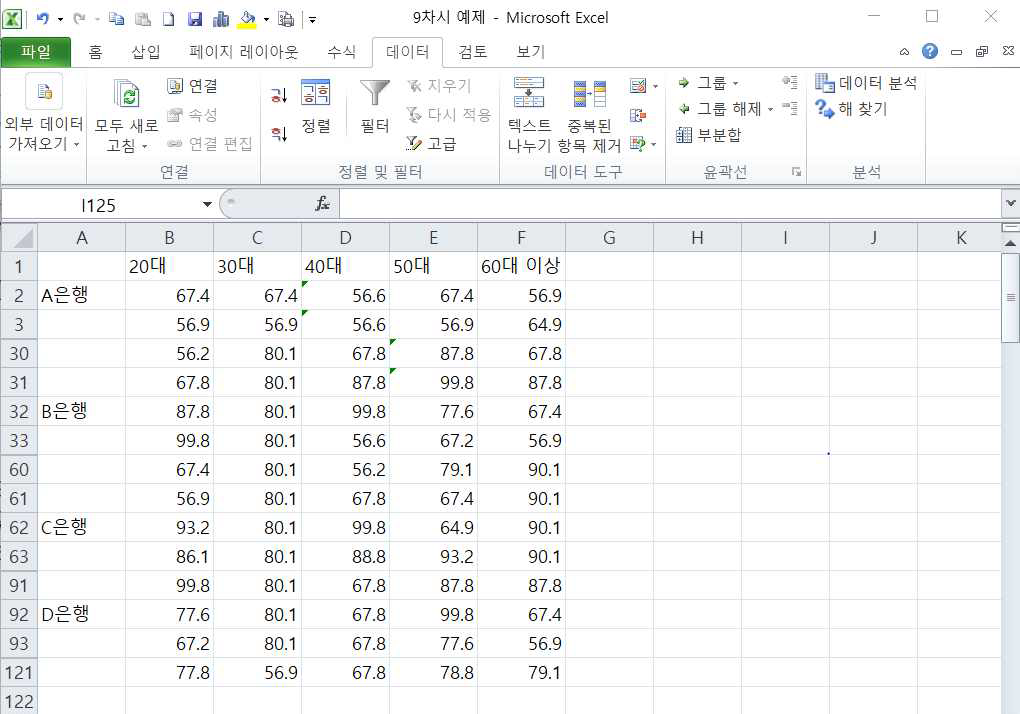
앞에서 반복이 없는 이원분산분석의 경우 데이터의 총변동(SST)를 요인A에 의한 제곱합(SSA), 요인B에 의한 제곱합(SSB), 잔차제곱합(SSE)로 분할하였으나 이와 같은 반복있는 분산분석은 각 처리수준에서 반복적인 측정이 되었기 때문에 교호작용 제곱합(SSAB)이 추가되어 분할됩니다.
따라서 반복 있는 이원 분산분석의 분산분석표는 다음과 같습니다.
단, 아래 표에서 r은 각 처리수준의 반복측정 표본수를 의미합니다.
※ 반복이 있는 이원분류 분산분석표
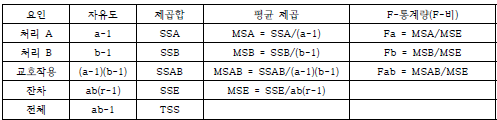
※ r : 각 처리별 표본수
※ 반복이 있는 이원분류 분산분석의 검정법

반복 없는 이원 분산분석과 마찬가지로 검정통계량 Fa = MSA/MSE가 기각치보다 크면 A요인의 처리별 평균이 모두 같다는 귀무가설을 기각하고, Fb = MSB/MSE가 기각치보다 크면 B요인의 처리별 평균이 모두 같다는 귀무가설을 기각합니다.
또한 가 기각치보다 크면 A요인과 B요인의 교호작용이 없다는 귀무가설을 기각하고, A요인과 B요인의 교호작용이 존재한다고 판단합니다.
이제 분산분석을 실행하기 위하여 데이터 → 데이터 분석 메뉴를 차례대로 선택하면 다음과 같은 데이터 분석 메뉴가 나타납니다.
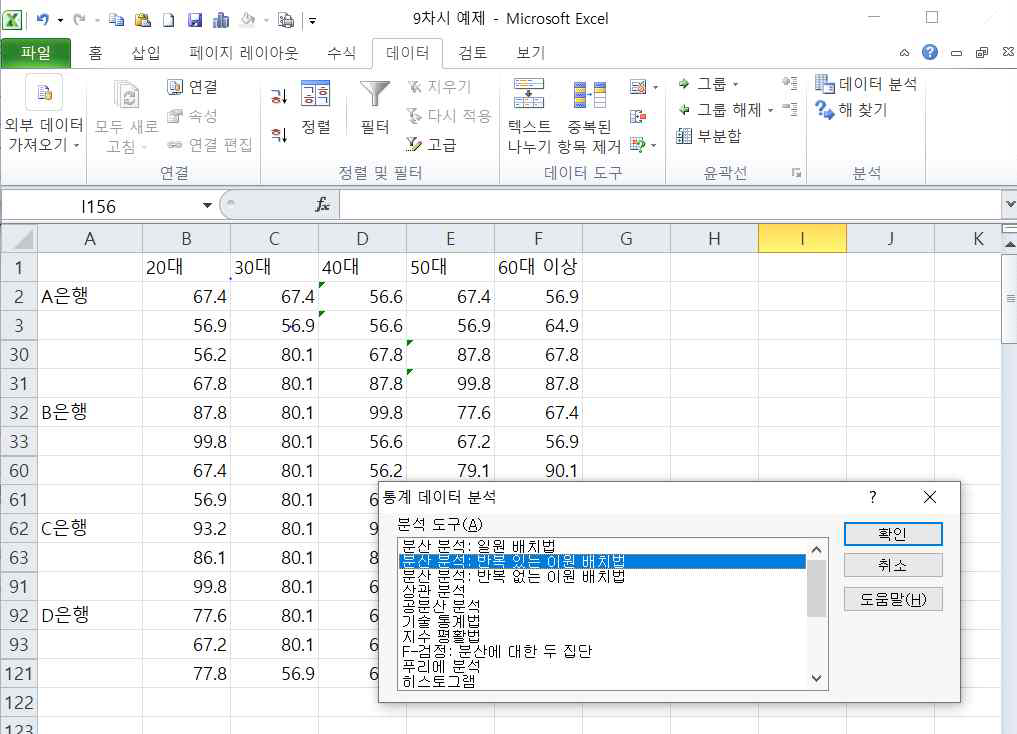
‘분산분석 : 반복 있는 이원 배치법’ 메뉴를 찾아서 확인을 클릭하면 데이터 범위 및 옵션을 입력하는 대화창이 나타납니다.
입력범위에 데이터 범위 a1:f121을 입력하고 표본당 행수에 각 처리수준별 반복측정 표본수인 30을 입력합니다. 유의수준은 0.05 출력옵션의 출력범위를 지정합니다. 여기서는 a124셀을 지정했습니다. 이제 확인을 클릭하면 결과가 나타납니다.
결과를 살펴보도록 하겠습니다.
먼저 각 은행별로 연령별 만족도 점수의 평균, 분산 등 기초 통계량이 제시됩니다.
A, B, D 은행은 40대의 점수가 낮고, C 은행은 연령별 큰 차이가 보이지않습니다. 또한 A, B, C, D 은행 전체의 평균은 각각 75.1, 76.4, 77.9, 74.6으로 큰 차이가 보이지 않습니다.
그러면 이제 크고 작은 차이들이 통계적 유의성이 있는 가에 대해서 분산분석표를 살펴보도록 하겠습니다.
먼저 요인 A(행_은행)에 의한 제곱평균(MSA)은 337.2, 잔차에 의한 제곱평균(MSE)은 139.3이므로 검정 통계량 Fa = MSA/MSE = 2.42로서 기각역 2.62보다 약간 작습니다. 또한 유의확률이 0.065로서 유의수준 0.05보다 약간 높게 나타났습니다.
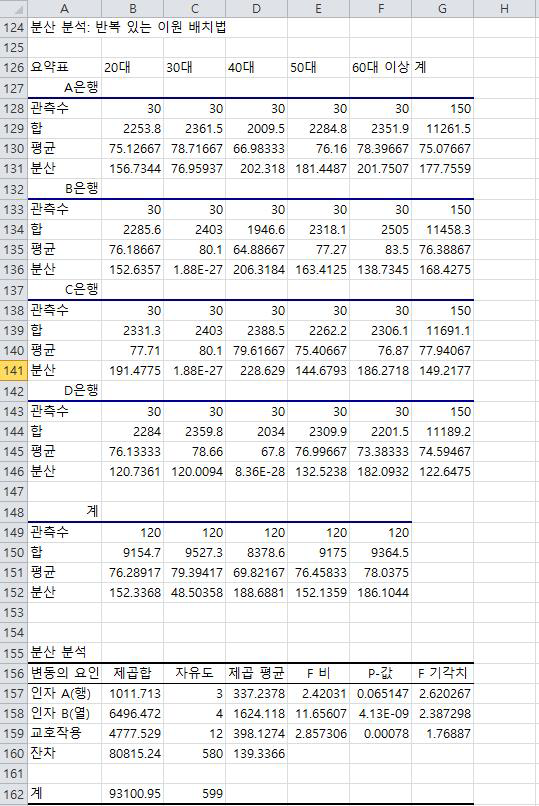
따라서 귀무가설을 기각하지 못하므로 은행 간 만족도의 평균값 차이는 통계적으로 유의하지 않다고 판단할 수 있습니다.
참고로 이때 유의수준을 10%로 한다면 유의수준 0.1보다 유의확률 0.065가 작기 때문에 귀무가설을 기각할 수 있습니다.
이렇게 동일한 데이터를 분석할 때 신뢰수준을 어느 정도로 하느냐에 따라 검정 결과가 달라질 수 있음에 유의해야 합니다.
다음은 요인B(열_연령)에 의한 제곱평균(MSB)이 1624.1, 잔차제곱평균(MSE)이 139.3이므로 검정 통계량 Fb = MSB/MSE = 11.65가 기각역 2.387보다 매우 큰 것을 볼 수 있습니다. 또한 유의확률은 4.13E-09로서 0.05보다 매우 작으므로 귀무가설을 기각할 수 있습니다. 즉, 연령별 모집단의 평균 차이가 통계적으로 유의할 정도로 다르다고 결론 내릴 수 있습니다.
이제 교호작용을 살펴보겠습니다. 교호작용에 의한 제곱평균(MSAB)가 398.1, 잔차제곱평균(MSE)이 139.3 이므로 검정통계량 Fab = MSAB/MSE = 2.86으로서 기각역 1.77보다 크게 나타났습니다. 또한 유의확률은 0.00078으로서 유의수준 0.05보다 작으므로 귀무가설을 기각할 수 있습니다. 즉, 은행 브랜드와 연령별 만족도의 통계적으로 유의한 교호작용이 존재하는 것으로 판단할 수 있습니다.
