F-test (F-검정)
두 집단 간 모분산의 동질성 검정
두 집단 간 모분산이 같은가에 대한 검정을 진행하기 위해서는 먼저 다음과 같은 가설이 설정될 것입니다.

예를 들어 다음은 A회사와 B회사의 브랜드 선호도에 대해서 각각 100명의 소비자들에게 5점 척도로 평가를 받은 데이터입니다. (참고로 엑셀에서 20행~99행 까지는 숨기기 처리를 한 화면입니다.)

이러한 2집단의 모분산 동질성을 검정하기 위해서는 다음과 같이 자유도 (n1-1, n2-1)인 F-검정 통계량을 사용합니다.

이제 위 검정 통계량을 구하기 위해 엑셀함수를 이용하여 수식을 따라 구해 보도록 하겠습니다.
1) 먼저 검정 통계량의 분자를 구하기 위해 ‘C열’에 각각의 (응답치 – 평균)을 입력하였습니다.
즉, C열-2행의 셀에 =A2-AVERAGE(A$2:A$101)와 같이 입력하였는데 이것은 (A회사 첫 번째 응답자의 평가치 - A회사 100명의 응답자 평균)를 구하라는 엑셀식입니다.
2) 그 다음은 D열-2행의 셀에 =POWER(C2,2)와 같이 입력하였는데 이는 C2셀의 제곱을 구하라는 엑셀식입니다.
즉, (A회사 첫 번째 응답자의 평가치 - A회사 100명의 응답자 평균)2을 구하라는 엑셀식입니다.
참고로 엑셀에 =power(a,b)는 ab를 구하라는 엑셀함수입니다.
3) 다음은 마우스로 c2셀과 d2셀을 잡고 101행까지 밑으로 끌면 동일한 수식이 그대로 적용되어 값이 구해집니다.
4) 다음은 D102셀에 =SUM(D2:D101)같이 입력하였는데 이는 D2셀~D101셀의 합,
즉 (A회사 i번째 응답자 평가치 - A회사 100명의 응답자 평균)2의 합을 구하라는 엑셀식입니다
5) 다음은 D103셀에 =99*D102와 같이 입력하면 위 검정통계량의 분자가 구해집니다.
6) 동일한 방법으로 B회사의 브랜드 선호도 점수를 구하면 F103셀에 위 검정 통계량의 분모가 구해집니다.
7) 분모와 분자를 나누어 검정 통계량값(2.5759)을 D104셀에 구했습니다.
이제 위 F-검정통계량의 기각역과 엑셀함수는 다음과 같습니다.

즉, 우측검정의 경우에 D105셀에 =FINV(0.05, 99, 99)와 입력하고 엔터를 치면 1.394라 는 기각치가 나타납니다.
좌측검정은 D106셀에 =FINV(0.95, 99, 99)라고 입력하면 0.717이라는 기각치가 나타납니다.
또한 위 검정통계량의 유의확률를 구하는 엑셀함수는 다음과 같습니다.

즉, D109셀에 =FDIST(D104, 99, 99)와 같이 입력하고 엔터를 치면 유의확률 1.99092E-6이 나타납니다.

이제 가설별로 기각역을 살펴보도록 하겠습니다.
먼저 검정통계량 2.5759 > 우측검정의 기각치 1.394이므로 귀무가설을 기각하고 A회사 평가치의 분산이 B회사 평가치의 분산보다 크다고 판단할 수 있습니다.
다음 검정통계량 2.5729 > 좌측검정의 기각치 0.717이므로 귀무가설을 기각하지 못합니다.
즉, A회사보다 B회사 평가치의 분산이 크다고 할 수 없습니다.
양측검정의 경우 검정통계량 2.5759 > 양측검정의 기각치 1.486 이므로 귀무가설을 기각하고 A회사와 B회사의 모분산은 같다고 할 수 없습니다.
이상과 같이 엑셀함수를 이용하여 두 집단 모분산 동질성을 검정할 수 있지만 데이터분석 → F-검정 : 분산에 대한 두 집단 메뉴를 차례로 선택하면 다음과 같은 대화창이 나타납니다.

A회사 평가 데이터와 B회사 평가 데이터 범위를 입력하고, 유의수준과 출력범위를 설정한 후 확인을 클릭하면 검정 결과가 나타납니다.
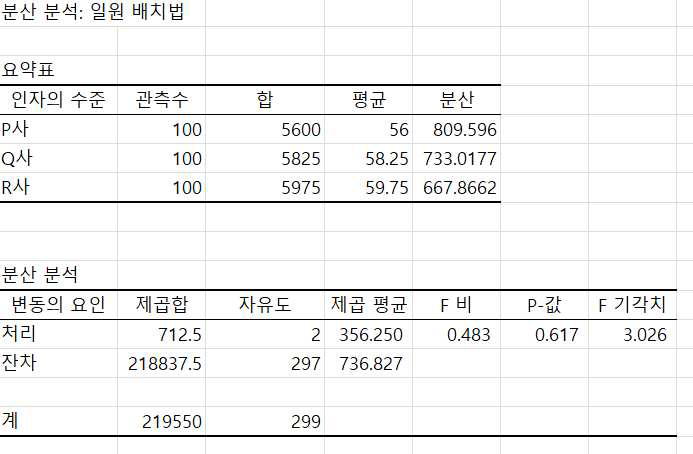
2개 회사에 대한 선호도 측정치의 평균값과 분산, 표본수 등의 기초통계량과 F-검정 통계량, 유의확률, F 검정의 기각치가 제시됩니다.
위에서 엑셀함수식으로 계산한 검정 결과와 동일하게 나타남을 볼수 있습니다.
엑셀에서 데이터분석 → ‘F-검정 : 분산에 대한 두집단’을 선택해서 검정을 실시하면 우측검정의 기각치만 제시합니다.
일변량 분산분석(One-way ANOVA)
앞에서 언급한 것처럼 분산분석은 3개 이상 집단의 평균 차이에 대한 검정방법에사용됩니다.
물론, 회귀분석 등에서 모델의 설명력 등을 분석할 때도 분산분석을 사용하지만 일변량 분산분석이란 한 개의 기준에 의하여 분류되는 여러 집단의 평균차이 검정에 사용되는 분석방법을 의미합니다.
예를 들어 5가지 브랜드의 신제품 컨셉에 대한 선호도, 3개 자동차 회사의 고객만족도 조사 점수, 특정 질병에 대한 4가지 치료약의 임상실험 결과 등의 모집단 평균점수에 대한 평균차이 검증을 할 때 사용하는 방법입니다.
이때 브랜드, 자동차 회사, 치료약 등과 같이 분류 기준이 되는 것을 분산분석에서는 ‘요인’이라 하고, 5가지 각각의 브랜드 3개 자동차 회사명, 4가지의 개별 치료제를 ‘처리’라고 칭합니다.

일변량 분산분석의 기본 개념은 전체 데이터의 변동량 중에서 처리에 의한 변동의 양이 차지하는 비율이 크면 모집단의 평균차이가 유의하다고 판단하는 방식입니다.
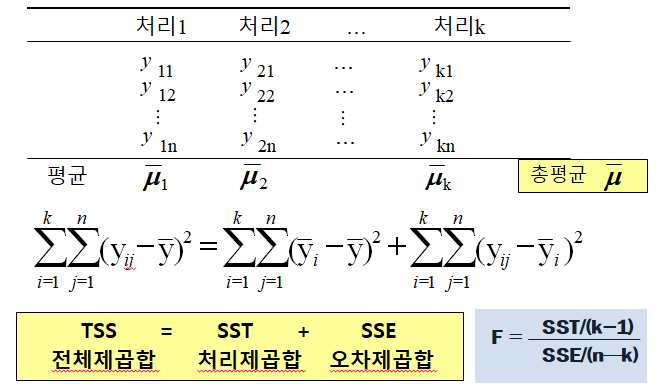
즉, 자료가 다음과 같이 측정되었다고 할 때 데이터의 전체 제곱합을 처리에 의한 제곱합과 오차에 의한 제곱합으로 나눈 다음 오차제곱합 평균 대비 처리제곱합 평균이 크면 모집단의 평균 간 처리가 모두 동일하지는 않다고 판단하는 접근 방식입니다.
여기서 처리제곱합 평균과 오차제곱합 평균의 비(ratio)를 검정통계량 F0로 사용합니다.
만약 k개 처리(집단)에 대한 평균차이 검정을 실사한다면 귀무가설, 대립가설과 이를 검정하는 유의확률, 기각치를 구하는 엑셀 함수식은 다음과 같습니다.

다음을 3개 자동차 회사의 고객만족도 점수라고 가정하고 3개 회사의 고객만족도 평균이 동일하다는 가정을 검정해 보도록 하겠습니다.
먼저 귀무가설과 대립가설은 다음과 같이 설정될 것입니다.

그런데 3개 이상 평균차이 검정을 실시하는 일변량 분산분석에서 검정통계량을 수식에 따라 엑셀함수식으로 구하는 것은 상당히 복잡한 작업을 반복해야 하므로 엑셀의 데이터 분석 메뉴를 이용하여 검정하도록 하겠습니다.
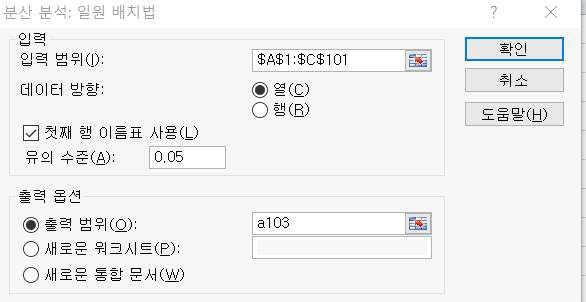
먼저 데이터분석 → ‘분산분석 : 일원배치법’을 클릭하면 다음과 같은 대화창이 나타납니다.
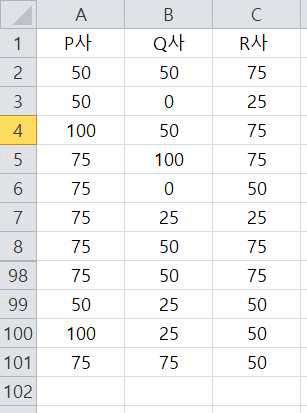
데이터가 입력되어 있는 범위를 입력해야 하는데 앞에서 공부한 T-검정처럼 각 변수의 데이터 범위를 따로따로 입력하는 것이 아니라 전체 데이터 범위를 묶어서 입력합니다.
즉, 일원 배치 분산분석에서는 ‘A1:C101“과 같이 변수명까지 묶어서 한 번에 데이터 범위를 입력합니다.
데이터 방향은 ‘열’로 선택하고, ‘첫 번 행 이름표 사용’을 체크하고 유의수준을 설정합니다.
만약 데이터 범위를 숫자 데이터의 범위인 ‘A2:C101’으로 입력한다면 ‘첫 번 행 이름표 사용’을 체크하지 않습니다. 그럴 경우 결과물에서 변수명이 P사, Q사, R사가 아닌 column1, column2, column3로 표시됩니다.
마지막으로 출력범위를 설정하고 확인을 클릭하면 결과가 나타납니다.
결과물을 살펴보도록 하겠습니다.
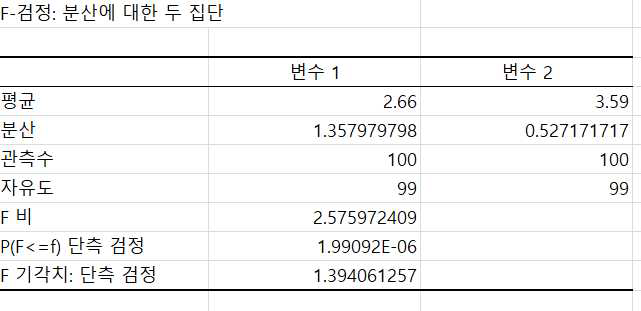
먼저 3집단의 평균, 분산 및 표본수 등의 기초 통계량이 출력되었습니다.
다음은 분산분석표가 제시되는데 처리제곱합(SST)이 712.5, 처리제곱평균값(MST)이 356.3
오차제곱합(SSE)이 218837.5 오차제곱평균값(MSE)이 736.8
Fo 검정통계량 = MST/MSE = 0.48로 나타났습니다.
기각치가 3.026 > 검정통계량 0.48이고 유의확률이 0.617 > 0.05 이므로 귀무가설을 기각하지 못합니다.
즉, 3개사의 고객만족도 평균 점수가 각각 56.0, 58,3 59.8로 나타났지만 통계적 유의성이 없으므로 3사의 고객만족도 점수는 서로 다르지 않다고 결론 내려야 하는 것입니다.
현재 적지 않은 여론조사나 고객만족도 조사 보고서에 이렇게 통계적 유의성 검정을 거치지 않고 단순 표본평균 점수만 가지고 R사 → Q사 → P사의 순으로 1등~3등으로 순위를 정하는 경우를 볼 수 있는데 이는 잘못된 분석과 보고서임을 유의해야 합니다. 표본 평균 점수는 모두 다르지만 그 차이가 크지 않아 통계적 유의성이 없음으로(귀무가설을 기각할 수 없으므로) 3사의 고객만족도 모평균 점수는 모두 차이가 없다는 식으로 결정이 되어야 하는 것입니다.