중위수와 최빈수(대푯값)
중심경향도의 이해
중심경향도란?
통계의 대상이 되는 표본이나 모집단 데이터를 대표할 수 있는 값으로, 데이터의 분포상 중심을 이루는 값이라고도 할 수 있습니다.
- 중심경향도, 중심경향치, 중심경향값, 중심값, 중앙값, 집중값, 중심화 경향 등으로 불림.
- 중심경향도를 보여주는 통계값 : 평균, 중위수, 최빈수
평균의 계산
평균은 가장 많이 사용되고 있는 중심경향도입니다.
평균의 종류: 산술평균, 기하평균, 조화평균
(여기서는 가장 대중적으로 사용되는 산술평균에 대해 알아보겠습니다.)
평균은 차이가 나는 데이터들의 값을 평평하게 만들어주는 값입니다.
평균값의 계산: 모든 데이터의 합계를 데이터의 수로 나눈 값.

평균값의 특징
계산이 간단하고 쉬움. 극단적인 값에 영향을 받음. 평균은 쉽게 계산할 수 있는 대표적인 데이터의 대푯값이지만, 극단적인 값에 영향을 받음.

평균값의 보안
이상치: 표본에서 대다수의 데이터와 큰 차이가 나는 특이한 소수의 데이터 이상치를 보안하는 방법
-평균에 영향을 미치는 큰 데이터 제외
-최댓값, 최솟값을 제외한 데이터로 평균을 계산

평균의 계산
엑셀을 활용한 평균 계산
엑셀 함수를 이용하면 평균값을 빠르고 쉽게 구할 수 있습니다.
평균 계산하는 엑셀 함수
AVERAGE, AVERAGEIF, AVERAGEIFS, TRIMMMEAN 등의 함수

1) AVERAGE – 산술평균법으로 여러 값들의 평균을 구하는 함수
응답자의 ‘출퇴근 소요시간’의 평균을 구하려면
=average(’출퇴근 소요시간(분)’의 모든 데이터)
2) AVERAGEIF – 서로 다른 조건을 가진 변수의 평균을 각각 구할 때
응답자의 ‘지역’으로 구분한 출퇴근 소요시간의 평균을 구하려면
=AVERAGEIF(출퇴근 소요시간(분)의 모든 데이터,“지방”)
=AVERAGEIF(출퇴근 소요시간(분)의 모든 데이터,“수도권”)
3) AVERAGEIFS – 2개 이상의 서로 다른 조건을 가진 변수의 평균을 각각 구할 때
응답자의 ‘지역’과 ‘성별’로 구분한 출퇴근 소요시간의 평균을 구하려면
=AVERAGEIFS(출퇴근 소요시간, 지역, “지방”, 성별, “여자”)
=AVERAGEIFS(출퇴근 소요시간, 지역, “지방”, 성별, “남자”)
할 비율)
4) TRIMMEAN – 측정값들을 크기로 나열했을 때 양 끝값을 제외한 부분의 평균을 구할 때
가장 큰 값과 가장 작은 값을 제외하고 구하는 평균을 구하려면
=TRIMMEAN(출퇴근 소요시간, 제외할 데이터의 비율)
중위수와 최빈수 계산
중위수란?
-중위수는 데이터의 값을 크기 순으로 나열했을 때 가운데에 오는 값. 중앙값, 메디안으로도 불림.
-데이터가 짝수일 때는 가운데에 위치하는 2개의 값을 합한 후 2로 나눈 값이 중위수.
-평균값에 비해 극단적인 값에 영향을 받지 않음.
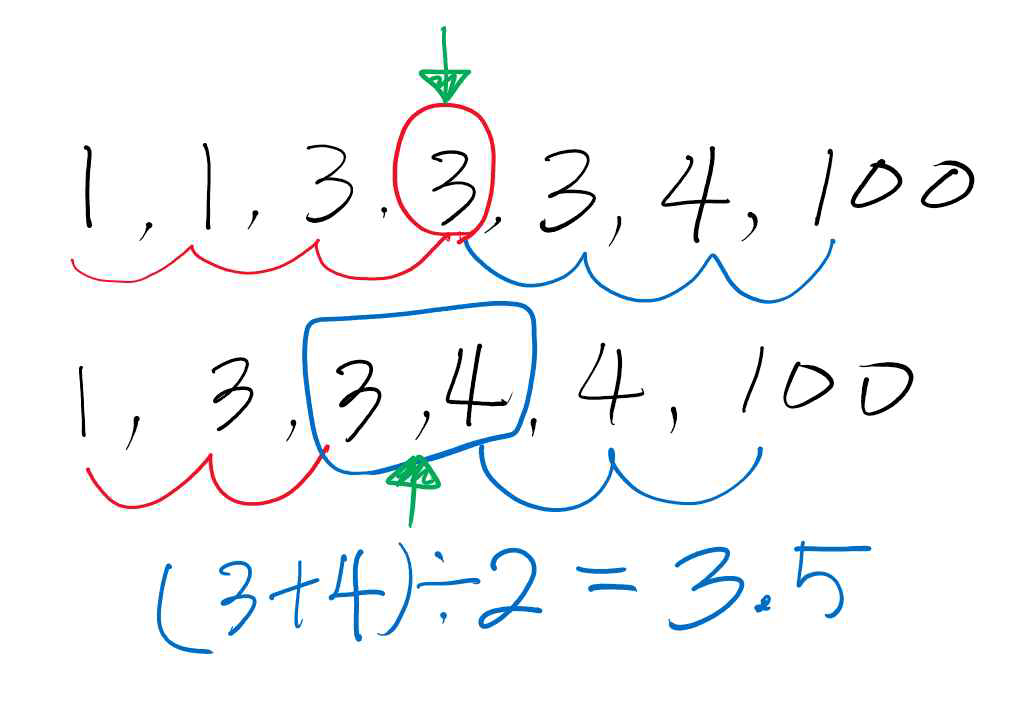
중위수를 구하는 함수
=Median(데이터의 범위)
최빈수란?
가장 자주 등장하는 데이터의 값. 질적 데이터의 대푯값은 유일하게 최빈수.
평균값에 비해 극단적인 값에 영향을 받지 않음.
최빈수를 구하는 함수
=Mode(데이터의 범위)
